Ebenen können im Raum auf verschiedene Arten zueinander liegen. Die verschiedenen Möglichkeiten sind folgende:
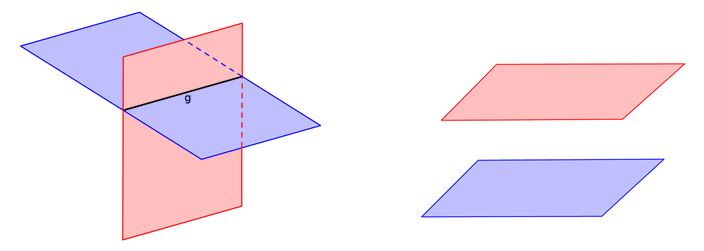
Mögliche Lagebeziehungen zwischen zwei Ebenen
Ebenen identisch: Jeder Punkt, der auf der einen Ebene ist, ist auch auf der anderen, es gibt unendliche viele Schnittgeraden.
Ebenen schneiden sich: Ebenen besitzen genau eine gemeinsame Schnittgerade, die alle Punkte, die auf beiden Ebenen liegen, enthält.
Ebenen echt parallel: Ebenen besitzen keine gemeinsamen Punkte und auch keine Schnittgerade.
Visualisierung der Lagebeziehungen
Schneidende Ebenen mit Schnittgerade | Zwei parallele Ebenen |
|---|
Bestimmung der Lagebeziehung (analytische Geometrie)
Auf diese Weise kann die Schnittgerade zweier Ebenen berechnet werden, sofern sie existiert, oder man kann zeigen, dass keine oder unendlich viele existieren:
Zur Berechnung braucht man eine Ebene in Koordinatenform,
und eine Ebene in Parameterform:
Falls die Ebenen nicht in der hier gebrauchten Form sind, hier können sie umgewandelt werden.
Vorgehensweise:
Einsetzen der Ebene in Parameterform in die Ebene in Koordinatenform. Hier wird die erste Zeile für in die Koordinatenform eingesetzt, die zweite Zeile für usw.
Erhaltene Gleichung vereinfachen
Versuche die Gleichung nach einer der beiden Variablen aufzulösen z.B. mögliches Ergebnis:
Aus dem Ergebnis der Gleichung folgt, welcher der oberen 3 Fälle vorliegt.
Liefert das Ergebnis…
... eine wahre Aussage, die nicht von und abhängt, z. B. von der Form : Beide Ebenen sind identisch, und alle Punkte der einen Ebene liegen in der anderen.
… eine für alle und falsche Aussage z. B. ist Ergebnis von der Form : Beide sind Ebenen echt parallel und haben keine gemeinsamen Punkte.
… eine Gleichung, die von und/ oder abhängt, z. B. in der Form : Die Ebenen schneiden sich und es gibt genau eine Gerade, auf der alle gemeinsamen Punkte liegen.
Beispiel: Schnittgerade bestimmen
Es ist
eine Ebene in Koordinatenform und
eine Ebene in Parameterform.
Setze in ein:
Wenn man nun in durch ersetzt, so erhält man die Gleichung der Schnittgeraden g:
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Lagebeziehung zweier Ebenen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
