Linearfaktordarstellung
Manchmal kann man eine Polynomfunktion komplett in Linearfaktoren aufspalten.
Aus unserer vorherigen Funktion wird dann zum Beispiel . (Wir benutzen dabei die erste binomische Formel.)
Diese komplett zerlegte Form hat einen besonderen Namen…
Diese Form nennt man die Linearfaktordarstellung von .
Dabei können durchaus mehrere N gleich sein. Dies ist zum Beispiel bei unserer Funktion der Fall.
Störe dich nicht an einem möglichen im Linearfaktor zum Beispiel bei . Dies kannst du ganz einfach in die Form bringen.
Der Faktor ist hier immer der Koeffizient der Potenz, die den Grad angibt (also die mit dem höchsten Exponenten). In unserem Beispiel ist die der Koeffizient von .
Zur besseren Übersicht lassen sich oft gleiche Linearfaktoren mithilfe einer Potenz zusammenfassen. Bei uns: .
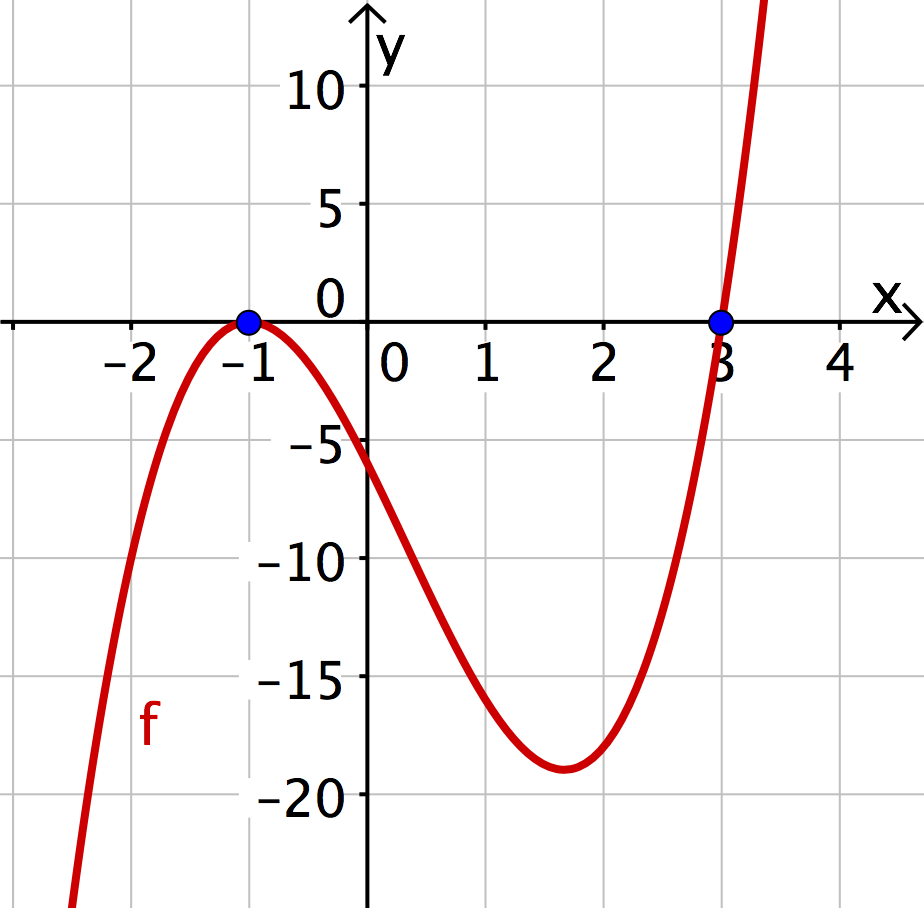
Ablesen von Nullstellen
An der Darstellung lassen sich nun alle Nullstellen ablesen:
An dem Linearfaktor lesen wir die Nullstelle ab; an den beiden Linearfaktoren lesen wir die Nullstelle ab.
Wie du siehst, hat die Linearfaktordarstellung einige Vorteile gegenüber der allgemeinen Darstellung .
