7Lineare (Un)abhängigkeit (2/2)
Drei Vektoren
Drei Vektoren a, b und c sind linear abhängig, wenn man eine Linearkombination mit ihnen bilden kann, sodass der Nullvektor entsteht:
(I)k1⋅a+k2⋅b+k3⋅c=0
Dabei ist (mindestens) einer der Koeffizienten ki von 0 verschieden.
Ist dagegen die Gleichung (I) nur erfüllbar, wenn alle ki den Wert 0 annehmen, dann sind die Vektoren a, b und c linear unabhängig.
Bildliche Veranschaulichung:
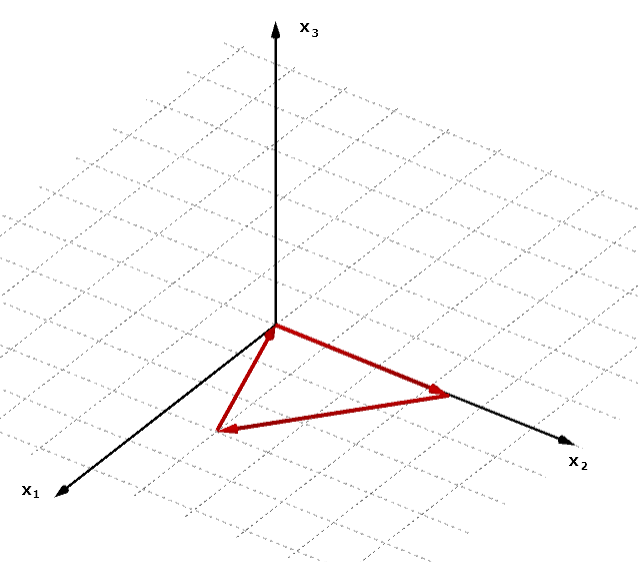
Linear abhängige Vektoren:
Die drei Vektoren liegen in einer Ebene.
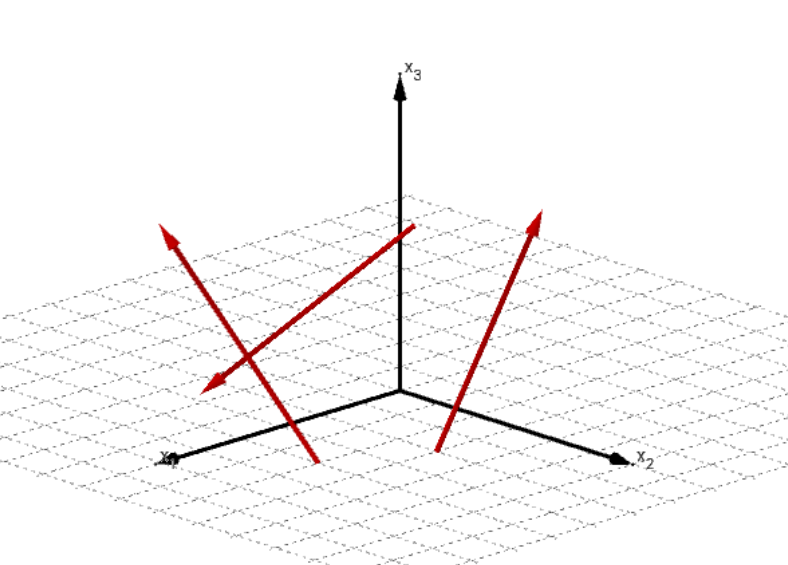
Linear unabhängige Vektoren:
Die drei Vektoren liegen nicht in einer Ebene.
Beispiel 1
Sind die drei Vektoren linear abhängig oder linear unabhängig?
1−23,12−1und101
Ansatz: Drei Vektoren sind linear abhängig, wenn man eine Linearkombination mit ihnen bilden kann, sodass der Nullvektor entsteht:
k1⋅1−23+k2⋅12−1+k3⋅101=000
Damit erhält man drei Gleichungen:
(I):(II):(III):k1−2k13k1++−k22k2k2+++k30k3===000
Aus (II)⇒k1=k2, eingesetzt in (I)und(III) erhält man die Gleichungen:
(I′):(III′):k13k1+−k1k1++k3k3==00⇒⇒2k12k1++k3k3==00
Rechnet man nun (I′)−(III′)⇒0=0
Das ist eine wahre Aussage und bedeutet, dass das Gleichungssystem unendlich viele Lösungen hat. Die drei Vektoren sind damit linear abhängig.
Möchte man eine Lösung des Gleichungssystems angeben, so kann z.B. k3=2 gesetzt werden. Aus (I′) folgt dann k1=−1 und aus (I) folgt k2=−1.
Beispiel 2
Sind die drei Vektoren linear abhängig oder linear unabhängig?
013,−111und211
Ansatz: Drei Vektoren sind linear abhängig, wenn man eine Linearkombination mit ihnen bilden kann, sodass der Nullvektor entsteht:
k1⋅013+k2⋅−111+k3⋅211=000
Damit erhält man ein Gleichungssytem, das man z.B. mit den Additionsverfahren lösen kann:
(I):(II):(III):0k13k1+++−k2k2k2+++2k3k3k3===000
Man rechnet z.B. (−3)⋅(II)+(III)⇒(I′) und (−2)⋅(I)⇒(II′)
(I′):(II′):00−+2k22k2−−2k34k3==00
(I′)+(II′):0k2−6k3=0⇒k3=0
k3=0 eingesetzt in (I)⇒k2=0
k3=0 und k2=0 eingesetzt in (II)⇒k1=0
Damit sind alle ki=0 , d.h. das Gleichungssystem hat nur die triviale Lösung.
Die drei Vektoren sind linear unabhängig.