Aufgaben zur Flächenberechnung von Parallelogrammen
- 1
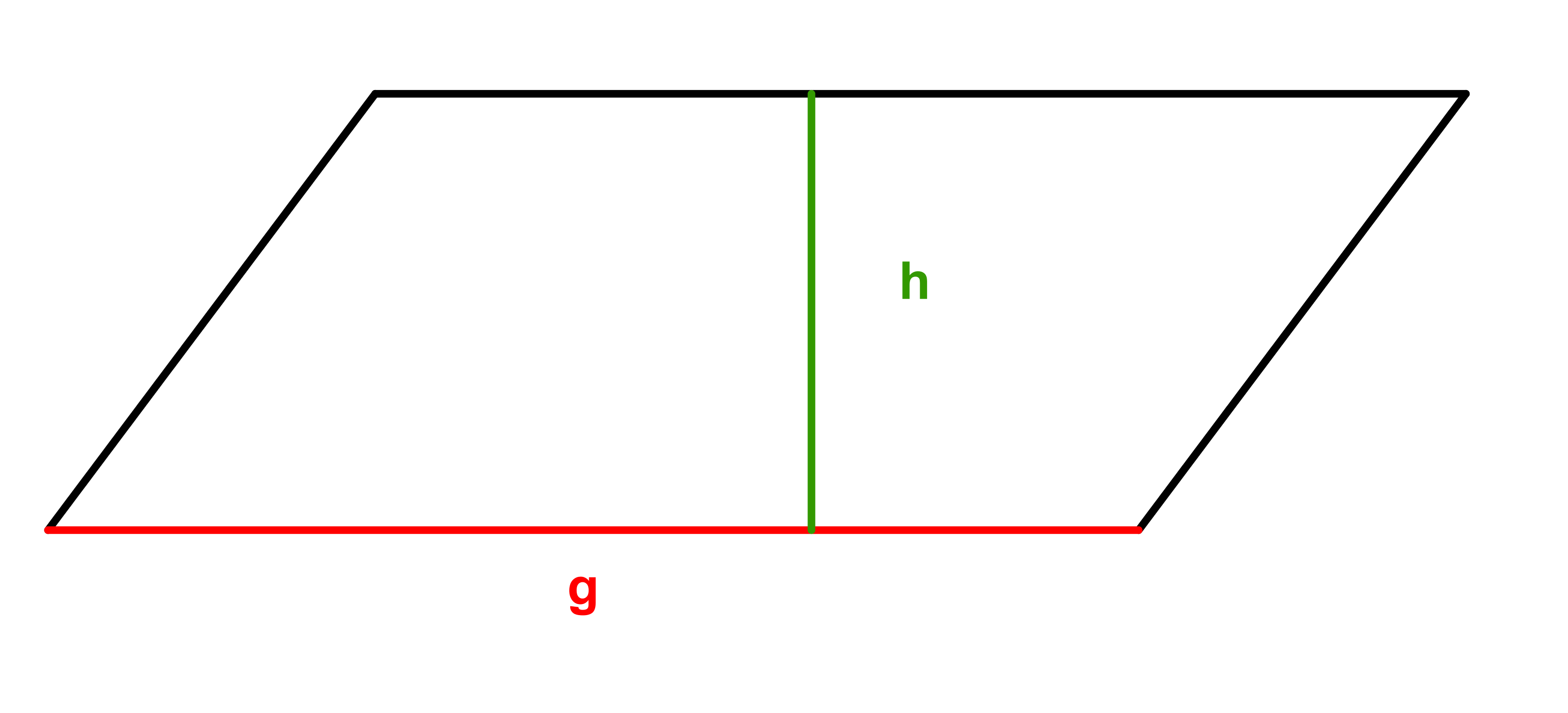
Berechne das Gesuchte im gegebenen Parallelogramm.
Gegeben ist die Höhe und der Flächeninhalt . Berechne die Grundlinie .
cmGegeben ist der Flächeninhalt und die Grundlinie . Berechne die Höhe .
cmGegeben ist die Grundlinie und die Höhe . Berechne den Flächeninhalt .
cm²Gegeben ist die Höhe und die Grundlinie . Berechne den Flächeninhalt .
cm²
- 2
Berechne die fehlenden Maße eines Parallelogramms.
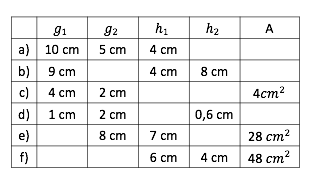
Gegeben:
gesucht:
Gegeben:
gesucht:
Gegeben:
gesucht:
Gegeben:
gesucht:
Gegeben:
gesucht:
Gegeben:
gesucht:
- 3
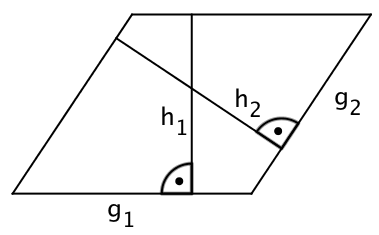
Ein Parallelogramm hat den Flächeninhalt und die Höhe . Der Umfang des Parallelogramms beträgt Berechne die Seitenlängen und und die Höhe .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
