Teil B, Gruppe 2
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Löse folgende Gleichung. (4 Punkte)
- 2
Mona und ihre Freundin Kati interessieren sich beide für Motorroller. (4 Punkte)
Mona bekommt folgende zwei Angebote:
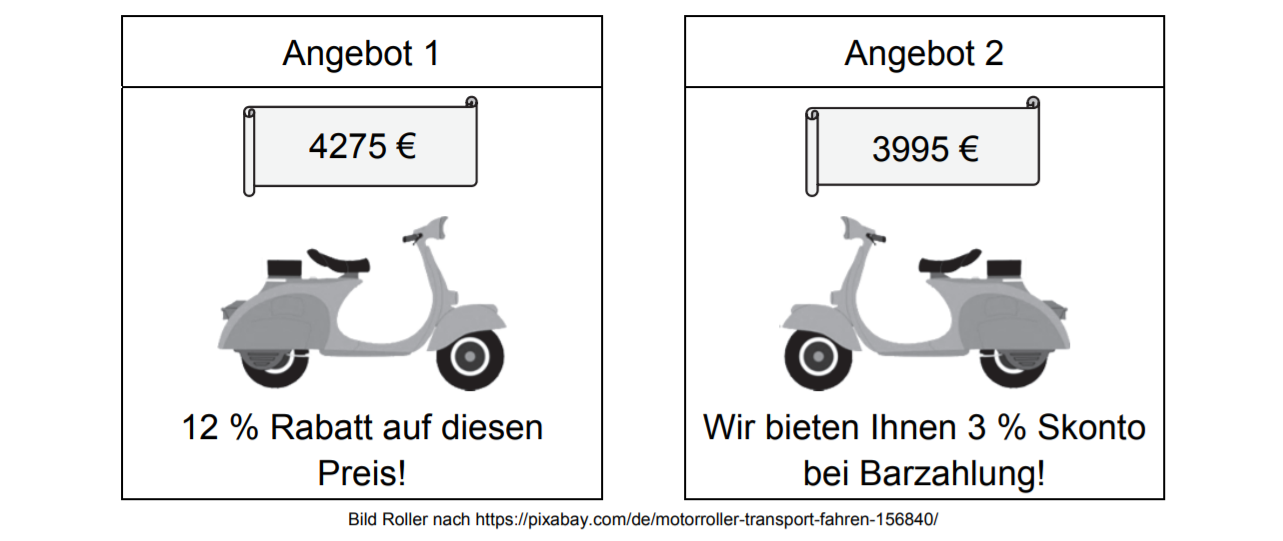
Grafik zu Angeboten
Ermittle, welches dieser beiden Angebote günstiger ist.
Kati kauft einen Roller, der von 4100 € auf 3567 € reduziert wurde.
Berechne, wie viel Prozent der Rabatt beträgt.
Um den Roller zu kaufen, muss Kati 10 Monate lang einen Kredit in Höhe von 3300 € zu einem Zinssatz von 4,5 % aufnehmen.
Berechne die tatsächlichen Anschaffungskosten für Katis Roller.
- 3
Die nachstehende Abbildung zeigt einen Richtungspfeil. (4 Punkte)
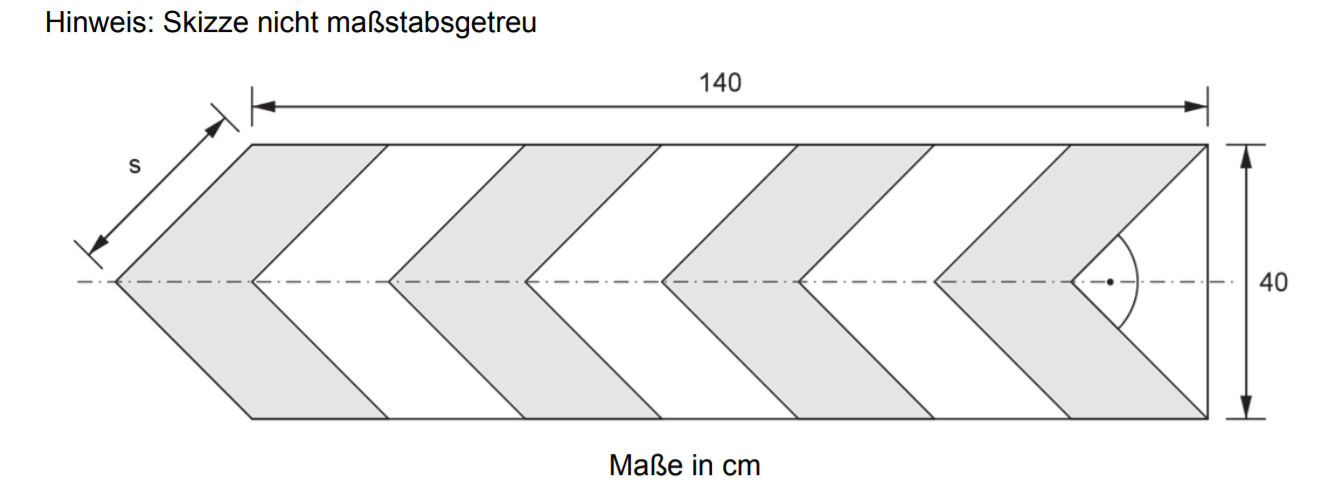
Pfeilskizze
Die dunkel gefärbten Flächen werden mit reflektierender Folie beklebt.
Berechne, wie viele Folie aufgeklebt werden.
Berechne die Länge der Strecke s in cm.
- 4
Aus einem Holzwürfel soll ein möglichst großer Zylinder hergestellt werden (siehe Skizze). (4 Punkte)
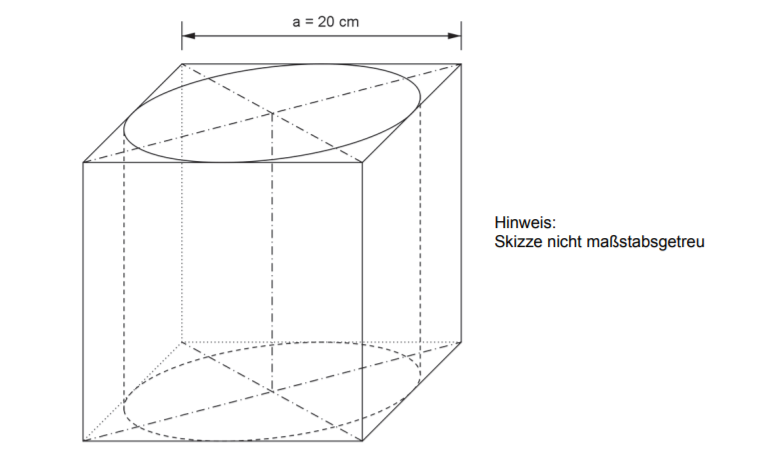
Zylinder aus Holzwürfel
Berechne das Volumen des Holzes, das dafür entfernt werden muss.
Ermittle den Oberflächeninhalt des entstehenden Zylinders.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
