Dieser Inhalt wurde gelöscht.
Die nachstehende Abbildung zeigt einen Richtungspfeil. (4 Punkte)
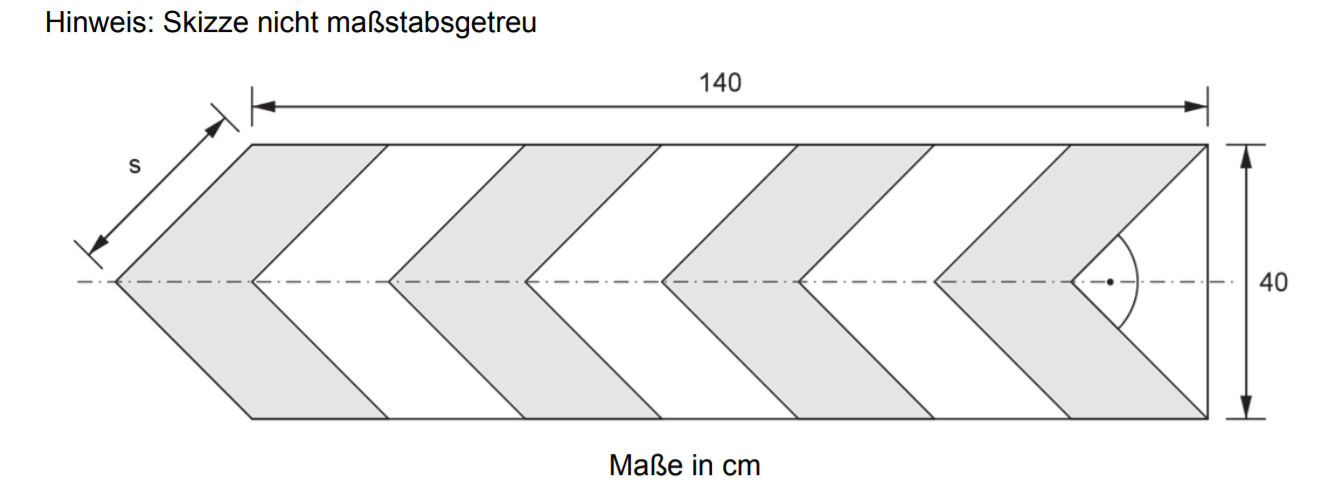
a) Die dunkel gefärbten Flächen werden mit reflektierender Folie beklebt.
Berechne, wie viele Folie aufgeklebt werden.
b) Berechne die Länge der Strecke s in cm.
