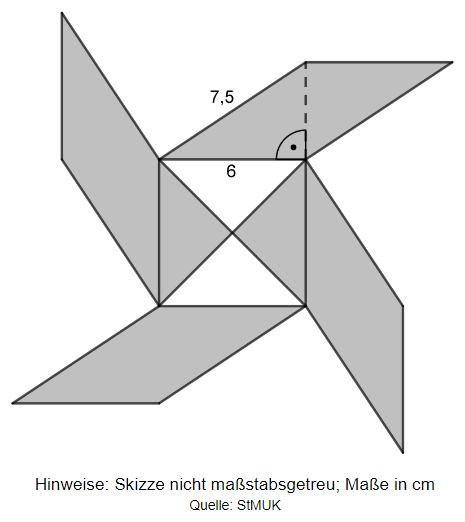
Die abgebildete Figur besteht aus einem Quadrat und vier deckungsgleichen Parallelogrammen.
Berechne den gesamten Inhalt der graumarkierten Fläche.
cm²
Die abgebildete Figur besteht aus einem Quadrat und vier deckungsgleichen Parallelogrammen.
Berechne den gesamten Inhalt der graumarkierten Fläche.
