Teil B, Gruppe 2
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
- 2
Ein Händler hat zwei Geschäfte, eines in Deutschland und eines in Österreich. In beiden Geschäften bietet er das gleiche Fernsehgerät an. Der Preis ohne Mehrwertsteuer beträgt in beiden Ländern 1500 € pro Gerät.
Im österreichischen Geschäft verkauft er ein Gerät einschließlich Mehrwertsteuer für 1800 €. Ermittle den österreichischen Mehrwertsteuersatz in Prozent.
%Wie viel kostet ein Gerät im deutschen Geschäft bei 19 % Mehrwertsteuer? Berechne diesen Preis.
€Herr Huber kauft ein anderes Fernsehgerät. Nach Abzug von 8 % Rabatt und 2 % Skonto zahlt er dafür 2073,68 €. Berechne seine Ersparnis für dieses Gerät in Euro.
 €
€
- 3
In einem Parallelogramm verbindet die Seite b die Eckpunkte B und C. Die Seitenlänge b beträgt 5 cm, die zugehörige Höhe und der Winkel .
Zeichne das Parallelogramm und beschrifte die Eckpunkte.
Berechne den Flächeninhalt des Parallelogramms.
cm²Ein Rechteck hat den doppelten Flächeninhalt wie dieses Parallelogramm.
Gib eine Möglichkeit für die Seitenlängen dieses Rechtecks an.
- 4
Für den Versand einer quadratischen Glaspyramide wird aus einem Schaumstoffwürfel mit der Kantenlänge ein passender Transportschutz hergestellt. Berechne das Volumen des Transportschutzes.
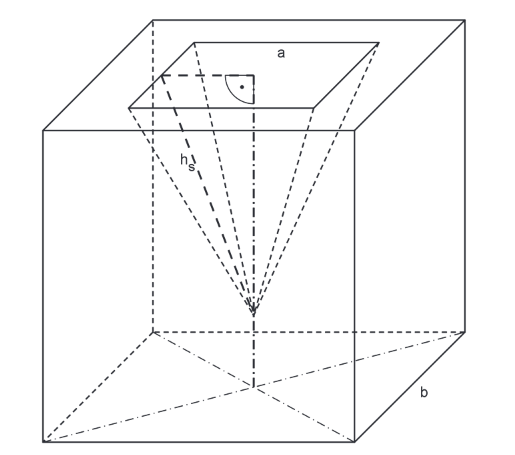
Hinweis: Skizze nicht maßstabsgetreu
cm³
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
