Nachtermin Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
Trapeze rotieren um die Achse . Die Winkel haben das Maß mit .
Es gilt: ; ; .
Die Zeichnung zeigt das Trapez für .
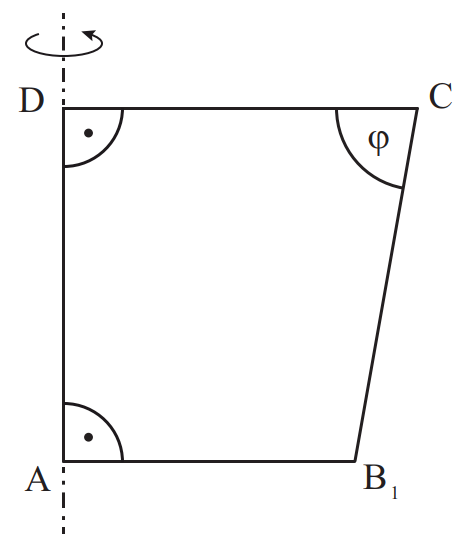
Zeichnen Sie das Trapez für in die Zeichnung ein.
(1 Punkt)
Bestätigen Sie die untere Intervallgrenze für und begründen Sie sodann, dass das Volumen der Rotationskörper gilt: .
(2 Punkte)
Zeigen Sie, dass für die Länge der Strecken in Abhängigkeit von gilt:
(2 Punkte)
- 2
Das radioaktive Isotop Cäsium-137 zerfällt mit einer Halbwertszeit von Jahren, d.h. nach dieser Zeit ist von einer bestimmten Anfangsmasse dieses Isotops nur noch die Hälfte an Cäsium-137 vorhanden. Der Zusammenhang zwischen der Anzahl der Jahre seit Beginn des Zerfalls und der Masse lässt sich näherungsweise durch eine Funktion der Form darstellen, wobei die Masse zu Beginn eines Versuches darstellt. Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Bei einem Langzeitversuch sind nach sechs Jahren noch des Isotops Cäsium-137 nachweisbar. Bestimmen Sie rechnerisch die Masse, die zu Beginn des Versuches vorhanden war.
(2 Punkte)
In einem anderen Versuch lässt sich der Zerfallsprozess durch die Funktion mit der Gleichung darstellen. Berechnen Sie, im wievielten Jahr erstmals weniger als des Isotops nachweisbar sind.
(2 Punkte)
Wie viel Prozent der ursprünglichen Masse des Isotops Cäsium-137 sind nach zehn Jahren noch vorhanden?
Kreuzen Sie die zutreffende Lösung an.
(1 Punkt)
a)
b)
c)
d)
e)
- 3
Der Punkt ist gemeinsamer Eckpunkt von gleichschenkligen Dreiecken
mit den Schenkeln und .
Die Mittelpunkte der Schenkel liegen auf der Geraden
mit der Gleichung . Es gilt: .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Zeichnen Sie die Gerade sowie die Dreiecke für und für
in das Koordinatensystem ein.
(Maße des Koodinatensystems: , )
Zeigen Sie, dass für die Länge der Strecken gilt: .
Unter den Dreiecken hat das Dreieck die kürzesten Schenkel.
Berechnen Sie die Koordinaten des zugehörigen Mittelpunktes des Schenkels .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
