Teil A
🎓 Prüfungsbereich für Bayern
Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite
Austausch & Hilfe:
Prüfungen-Discord
Die Aufgabenstellung findest du hier zum Ausdrucken als PDF.
- 1
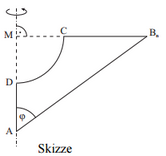
Gegeben sind rechtwinklige Dreiecke mit und den Hypotenusen .
Die Winkel haben das Maß mit .
Der Kreis mit dem Mittelpunkt und dem Radius schneidet die Seite im Punkt und die Seiten im Punkt .
Runden Sie im Folgenden auf zwei Stellen nach dem Komma.
Berechnen Sie die Länge der Seite für .
Die Figuren , die durch die Strecken und sowie durch den Kreisbogen begrenzt wird, rotieren um die Gerade .
Zeigen Sie durch Rechnung, dass für das Volumen der entstehenden Rotationskörper in Abhängigkeit von gilt:
Berechnen Sie das Volumen des entstehenden Rotationskörpers für
- 2
Punkte mit legen zusammen mit den Punkten und Parallelogramme fest.
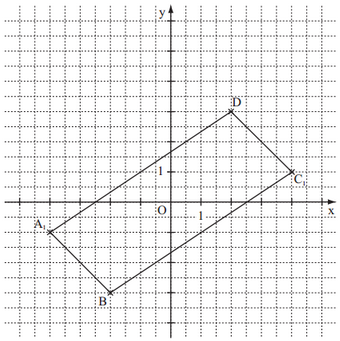
In das Koordinatensystem zur Aufgabenstellung ist das Parallelogramm für eingezeichnet.
Berechnen Sie die Koordinaten des Punktes für und zeichnen Sie sodann das Parallelogramm ein.
Zeigen Sie rechnerisch, dass für den Trägergraphen der Punkt gilt:
.
Zeichnen Sie den Trägergraphen in das Koordinatensystem zur Aufgabenstellung ein.
Begründen Sie, dass die Flächeninhalte aller Parallelogramme maßgleich sind.
- 3
Gegeben ist die Funktion mit der Gleichung .
Geben Sie die Definitionsmenge der Funktion an.
Bestimmen Sie die nach aufgelöste Gleichung der Umkehrfunktion zu .
Der Graph der Funktion hat eine Gleichung der Form und schneidet den Graphen der Funktion auf der -Achse.
Bestimmen Sie den zugehörigen Wert für .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
