Weitere Aufgaben zu Extremwertproblemen
Hier findest du Aufgaben zu Extremwertproblemen. Lerne das Optimieren mithilfe von Extremwertproblemen!
- 1
Welcher Punkt auf der Geraden g mit der Funktionsgleichung hat vom Punkt minimalen Abstand?
Wie groß ist dieser minimale Abstand?
Fertige zunächst eine Skizze an!
- 2
Welcher Punkt P auf der Parabel mit der Funktionsgleichung hat vom Punkt minimalen Abstand?
Wie groß ist dieser minimale Abstand?
- 3
Der Absatz (Verkaufszahlen) einer Ware ist wesentlich abhängig vom Preis . Je höher der Preis, desto geringer ist in der Regel der Absatz.
Diesen Zuammenhang beschreibt die Preis-Absatz-Funktion (PAF)
Der Umsatz (Verkaufserlös) ist als Produkt aus Absatz und Preis eine Wertgröße.
Eine Firma verkauft pro Monat von einem Artikel Stück zu einem Stückpreis von .
Die Preis-Absatz-Funktion ist gegeben durch:
Bestimme den monatlichen Umsatz in Abhängigkeit vom Stückpreis p.
Für welchen Preis p ist der Umsatz maximal?
- 4
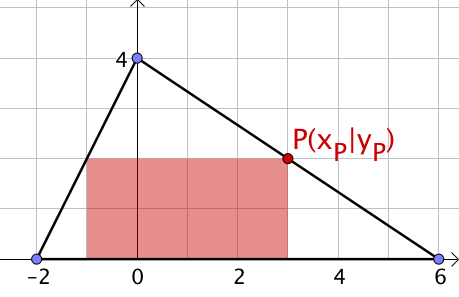
Dem abgebildeten Dreieck soll ein Rechteck mit möglichst großem Flächeninhalt einbeschrieben werden.
Berechne den größtmöglichen Flächeninhalt.
- 5
Es gibt viele Zahlenpaare positiver Zahlen, deren Produktwert 0,64 beträgt.
a) Gib 10 solcher Zahlenpaare an.
b) Ermittle dasjenige Zahlenpaar, das den kleinsten Summenwert besitzt.
- 6
Aus einer rechteckigen Fensterscheibe mit den Seitenlängen und , ist vom unteren Mittelpunkt der kleineren Seite aus, eine Ecke geradlinig unter einem Winkel von 45° abgesprungen.
Aus der restlichen Scheibe soll durch Schnitte parallel zu den ursprünglichen Seiten eine möglichst große rechteckige Scheibe hergestellt werden.
Welche Seitenlängen und welche Fläche hat die "Ersatzscheibe"? In welchem Punkt setzen die Schnitte an?
- 7
Aus einem kreisrunden Papierstück mit dem Radius R soll eine kegelförmige Popkorntüte hergestellt werden.
Wie muss das Papier zugeschnitten und zusammengeklebt werden, wenn die fertige Tüte mit möglichst viel Popcorn gefüllt werden soll?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
