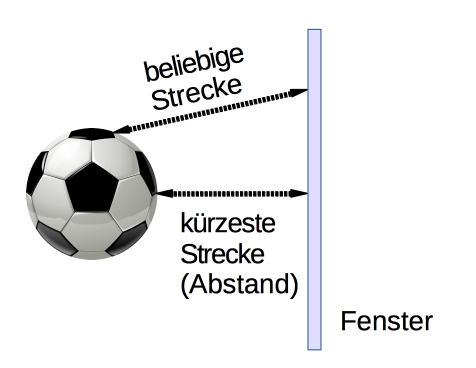
Man stellt sich zwei Objekte vor (zum Beispiel einen Ball und ein Fenster). Auf jedem Objekt wählt man je einen Punkt und misst die Strecke zwischen beiden Punkten. Der Abstand ist nun die Länge der kürzesten Strecke, die man auf diese Weise finden kann.
Überblick über die verschiedenen Abstandsberechnungen
Eigenschaften
Ein Abstand ist immer eine nichtnegative Zahl, also .
Er stellt immer die kürzeste Verbindung zweier Objekte dar
Umwege über einen weiteren Punkt sind nicht kürzer
