Springe zum Inhalt oder Footer
SerloDie freie Lernplattform

Winkelsumme

Bild

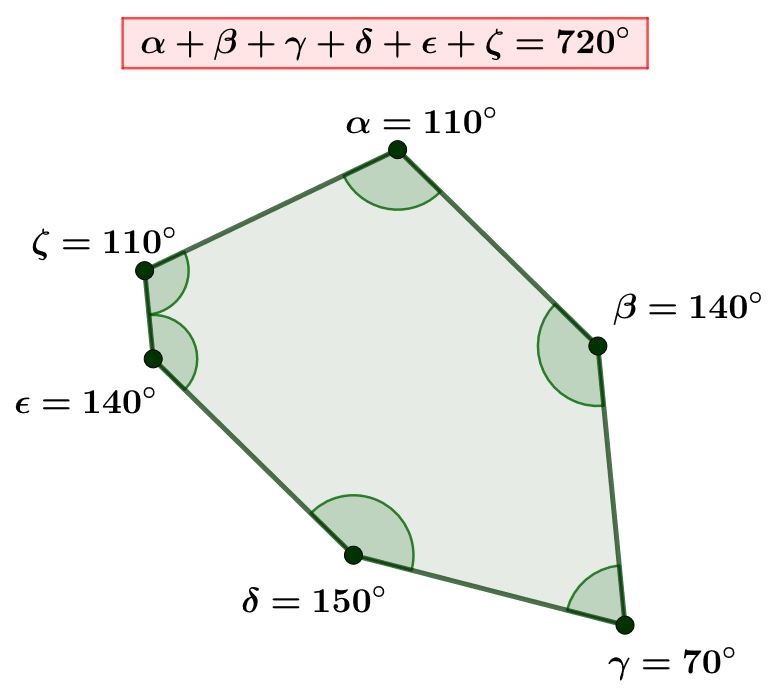
Die Winkelsumme bezeichnet den Wert, den alle Winkel eines nn-Ecks zusammenaddiert ergeben.

Sie ist in beliebigen n-Ecken gegeben durch die Formel:

Beispieln-Ecke

  • Dreieck: n=3n=3:  Winkelsumme=(3−2)⋅180∘=180∘Winkelsumme=(3-2)\cdot180^\circ=180^\circ

  • Viereck: n=4n=4:  Winkelsumme=(4−2)⋅180∘=2⋅180∘=360∘Winkelsumme=(4-2)\cdot180^\circ=2\cdot180^\circ=360^\circ

  • Fünfeck: n=5n=5: Winkelsumme=(5−2)⋅180∘=3⋅180∘=540∘Winkelsumme=(5-2)\cdot180^\circ=3\cdot180^\circ=540^\circ

Übungsaufgaben

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel


Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?