Die Ordnungskraft der Mittelpunkte
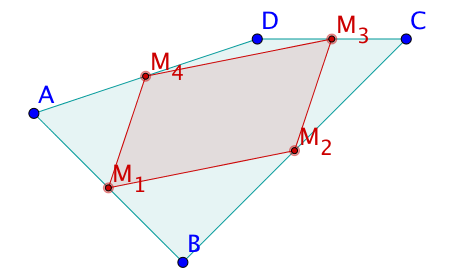
Ein allgemeines Viereck . Die Seiten des Vierecks sind weder parallel noch gleich lang.
Verbindet man die Mittelpunkte der Vierecksseiten zu einem neuen Viereck, entsteht das "Mittelpunktsviereck". Das Mittelpunktsviereck ist stets ein Parallelogramm.
Begründe die "Ordnungskraft" der Seitenmittelpunkte eines Vierecks: Erkläre, warum das Mittelpunktsviereck eines beliebigen Vierecks stets ein Parallelogramm ist.
Von welcher Form sind die Mittelpunktsvierecke von Quadraten? Begründe deine Antwort!
Von welcher Form sind die Mittelpunktsvierecke von Rechtecken? Begründe deine Anwort!
Von welcher Form sind die Mittelpunktsvierecke von Rauten? Begründe deine Anwort!
