Denk- und Beweisaufgaben zum Parallelogramm
Wie gut kennst du dich mit dem Parallelogramm aus? Teste dich mit diesen Denkaufgaben und vertiefe dein Wissen!
- 1
Experimentiere mit einem Zollstock

Mit einem Zollstock lassen sich leicht verschiedene Parallelogramme formen.
Durch die Seitenlängen (und somit auch durch seinen "Umfang", d.h. die Summe der Seitenlängen) ist die Form eines Parallelogramms nicht bestimmt. Zeige dies!
Welche Form besitzt ein Parallelogramm mit vorgegebenen Seitenlängen, wenn seine beiden Höhen am größten sind?
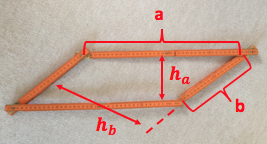
Was passiert mit der Höhe eines bestimmten "Zollstockparallelogramms", wenn man dieses ohne Veränderung der Seitenlängen so verbiegt, dass die Höhe nur noch die Hälfte (den dritten Teil; den vierten Teil) beträgt?
Wahr oder falsch?
Wird ohne Veränderung der Seitenlängen eine Höhe eines Parallelogramms um (, ) kleiner, dann wird auch die andere Höhe um (, ) kleiner.
- 2
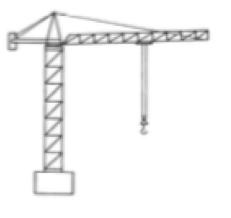
Große Lasten - hohe Kräfte!
Ein Parallelogramm, bei dem nur die Seitenlängen vorgegeben sind, ist nicht "stabil".
Falls jedoch zusätzlich noch eine Diagonalenlänge fest gegeben ist, "rührt" sich an dem Parallelogramm nichts mehr.
Probiere es z.B. an einem Zollstockparallelogramm aus.
In der Technik nennt man solch eine stabilisierende Diagonale eine "Verstrebung" und erreicht damit große Belastbarkeit, etwa bei Baukränen.
Kannst du dir erklären, warum solch eine Verstrebung funktioniert?
- 3
Konstrukteure gefragt
Geometrische Aufgaben löst man in der Regel durch eine Berechnung oder durch eine Konstruktion.
Eine "Konstruktion" ist eine möglichst genaue Zeichnung alleine mit den Hilfsmitteln eines Zirkels und eines Lineals. Oft darf man zur Erleichterung auch ein Geodreieck verwenden.
Löse die folgenden Aufgabenstellungen jeweils durch eine Konstruktion.
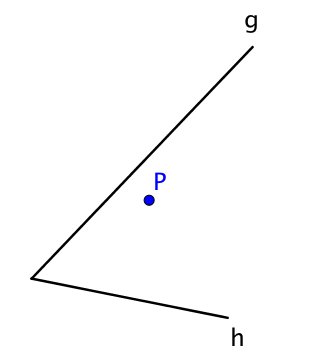
Konstruiere eine Strecke durch den Punkt P als Mittelpunkt der Strecke so, dass die Endpunkte auf g und h liegen.
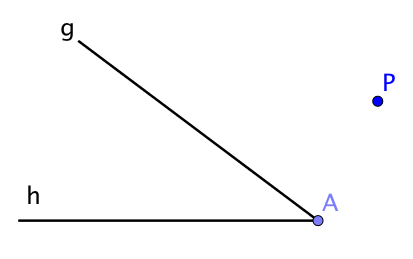
Lege eine Strecke von P aus so, dass der Endpunkt auf h liegt und die Strecke von g halbiert wird.
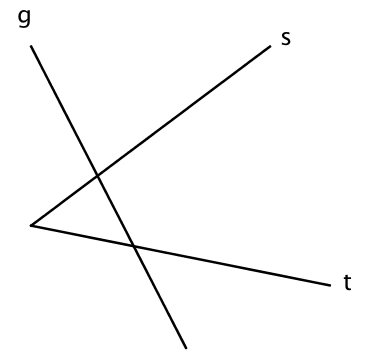
Konstruiere eine zur Geraden g parallele Strecke mit vorgegebener Länge a LE so, dass die Endpunkte der Strecke auf s und t liegen.
- 4
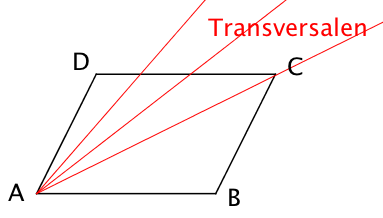
Quer durchs Parallelogramm
Eine Gerade "quer" durchs Parallelogramm, wie z.B. eine Diagonale, heißt eine Transversale.
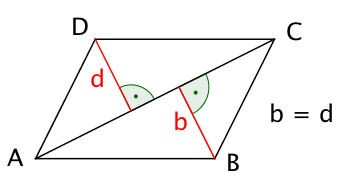
Begründe, warum die Eckpunkte B und D des Parallelogramms ABCD von der Diagonalen durch A und C gleichen Abstand haben.
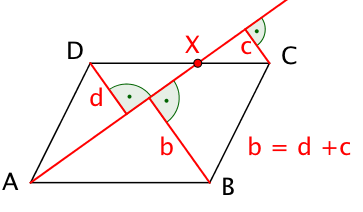
Für eine durch den Eckpunkt A des Parallelogramms ABCD und einen beliebigen Punkt X der Seite [CD] verlaufende Transversale gilt:
Der Abstand des Punktes B zur Transversalen ist die Summe der Abstände der Eckpunkte C und D von ihr.
Begründe dies.
Was gilt für die Teilaufgabe b, wenn X = D?
Was gilt, wenn X = C?
- 5
Verwandlungskünste
Je weniger Eckpunkte eine geometrische Figur bei gleichbleibender Fläche hat, desto wünschenswerter ist dies oft.
Verwandle durch eine Konstruktion Parallelogramme so, dass jeweils ein flächengleiches Dreieck entsteht.
Verwandle das Parallelogramm mit den Eckpunkten unter Beibehaltung der Seite und des Innenwinkels in ein flächengleiches Dreieck.
Verwandle das Parallelogramm mit den Eckpunkten unter Beibehaltung der Parallelogrammseite und des Innenwinkels in ein flächengleiches Dreieck.
- 6
Geometrische Graffitis
Zur Verschönerung wird ein Parallelogramm auf drei verschiedene Weisen mit geometrischen Figuren besprüht. (Welches Graffiti würde dir als "Kunstwerk" am besten gefallen?)
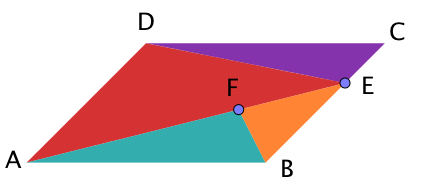
Graffiti 1
Hier gilt:
und
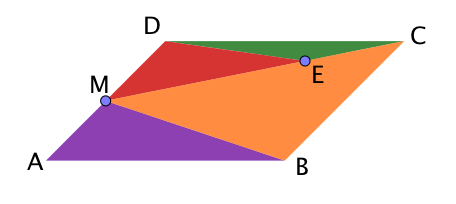
Graffiti 2
Hier gilt:
und
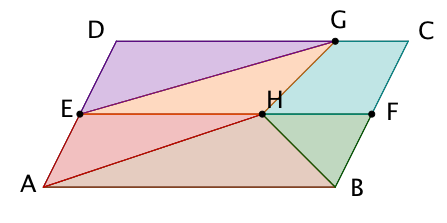
Graffiti 3
Hier gilt:
ist eine Mittelparallele im Parallelogramm und der Punkt teilt diese im Verhältnis . Der Punkt teilt die Seite im Verhältnis .
Schule dein Empfinden für Flächengrößen und entscheide ohne Rechnung, welche Aussage für das Graffiti 1 zutrifft.
Klicke die deiner Meinung nach zutreffende Aussage an.
Entscheide auch für das Graffiti 2 ohne Rechnung, welche der folgenden Aussagen zutrifft.
Klicke die deiner Meinung nach richtige Aussage an.
Ordne für das Graffiti 1 die Teilflächen der Größe nach und beweise, dass sie im Verhältnis stehen.
Ordne für das Graffiti 2 die Teilflächen der Größe nach und beweise, dass sie im Verhältnis stehen.
Beweise, dass das Graffiti drei gleich große Teilflächen enthält und die drei anderen im Verhältnis stehen.
- 7
Die Ordnungskraft der Mittelpunkte
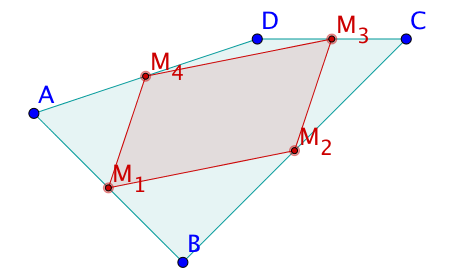
Ein allgemeines Viereck . Die Seiten des Vierecks sind weder parallel noch gleich lang.
Verbindet man die Mittelpunkte der Vierecksseiten zu einem neuen Viereck, entsteht das "Mittelpunktsviereck". Das Mittelpunktsviereck ist stets ein Parallelogramm.
Begründe die "Ordnungskraft" der Seitenmittelpunkte eines Vierecks: Erkläre, warum das Mittelpunktsviereck eines beliebigen Vierecks stets ein Parallelogramm ist.
Von welcher Form sind die Mittelpunktsvierecke von Quadraten? Begründe deine Antwort!
Von welcher Form sind die Mittelpunktsvierecke von Rechtecken? Begründe deine Anwort!
Von welcher Form sind die Mittelpunktsvierecke von Rauten? Begründe deine Anwort!
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
