Aufgaben zur Berechnung von Längen im Koordinatensystem
Lerne hier, den Abstand zwischen Punkten zu berechnen und die Länge von Strecken im Koordinatensystem zu bestimmen.
- 1
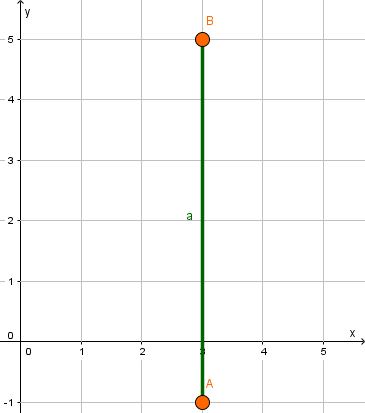
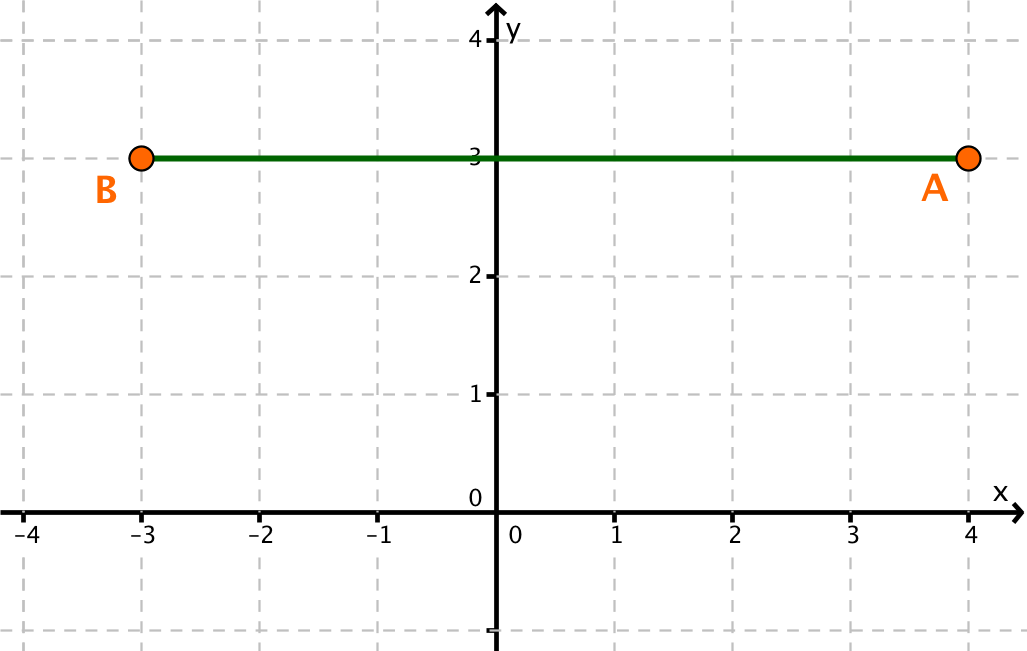
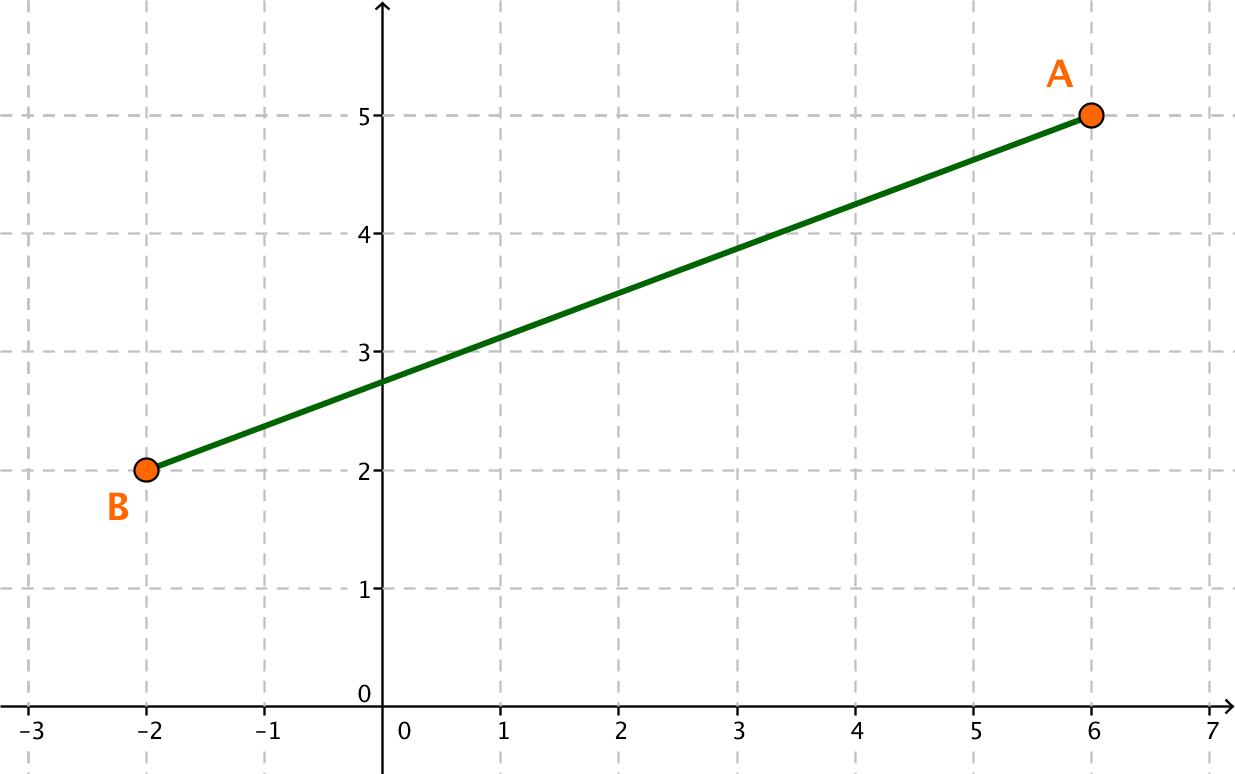
Berechne die Länge der Strecke mithilfe der angegebenen Koordinaten
A(2|8), B(2|2)
A(-3|-2), B(5|-2)
A(-2|3), B(1|-1)
- 2
Berechne die Länge der Strecke .
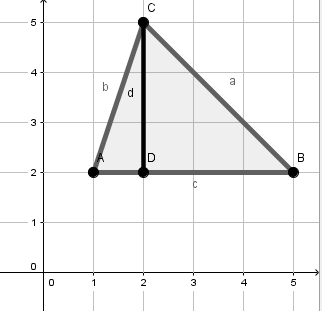
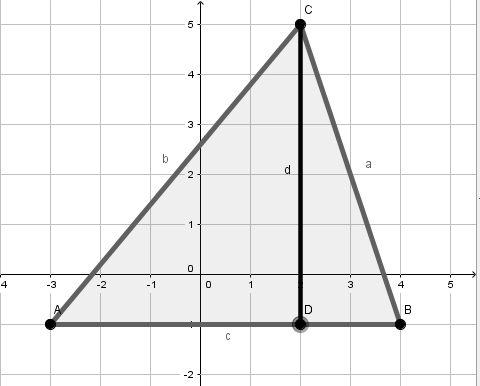
- 3
Berechne die Längen der Strecken a,b,c und d
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?