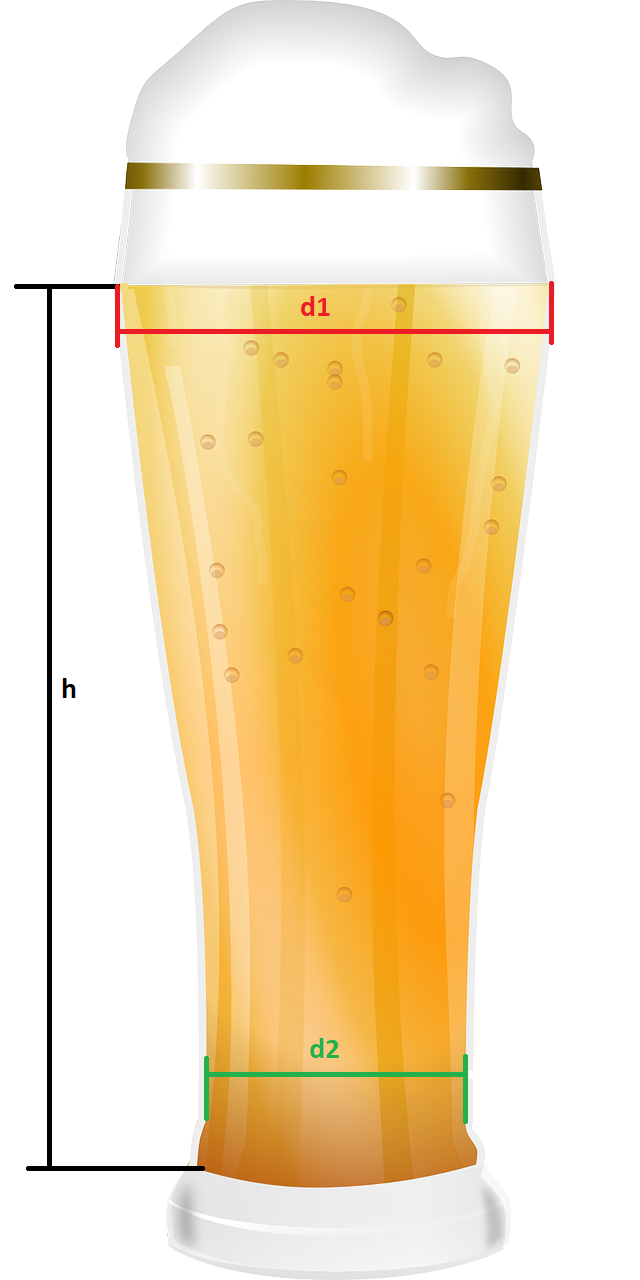
Ein Weißbierglas hat bis zur Eichmarkierung eine Füllhöhe von . Außerdem hat es den maximalen Durchmesser und den minimalen Durchmesser .
Schätze mit diesen Zahlen das wahre Volumen des Gefäßinhaltes nach oben und nach unten ab.

Ein Weißbierglas hat bis zur Eichmarkierung eine Füllhöhe von . Außerdem hat es den maximalen Durchmesser und den minimalen Durchmesser .
Schätze mit diesen Zahlen das wahre Volumen des Gefäßinhaltes nach oben und nach unten ab.