7Beispiel: Streckung in x-Richtung

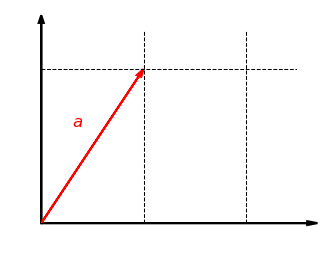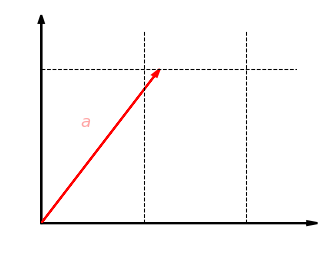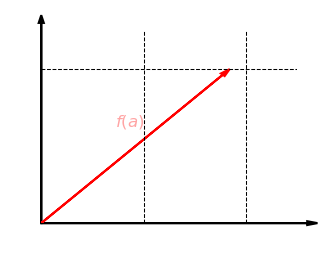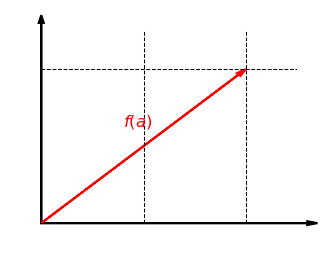
Unser erstes Beispiel ist die Streckung um den Faktor $\beta$ in $x$-Richtung in der Ebene $\R^2$. Dabei wird jeder Vektor $a=(a_x, a_y)^T \in\R^2$ abgebildet auf $f(a)=(\beta a_x, a_y)^T$. Die folgende Grafik zeigt diese Abbildung für $\beta = 2$. Die $y$-Koordinate bleibt dabei gleich und die $x$-Koordinate wird verdoppelt:

Schauen wir uns nun an, ob diese Abbildung verträglich mit der Addition ist. Nehmen wir also zwei Vektoren $a$ und $b$, bilden die Summe $a+b$ und strecken diese dann in $x$-Richtung. Das Ergebnis ist dasselbe, als wenn wir beide Vektoren zuerst in $x$-Richtung strecken und dann addieren:

Das lässt sich auch mathematisch zeigen. Unsere Abbildung ist die Funktion $f: \R^2 \to \R^2, \ f(\left(x, y)^T\right)=(\beta x, y)^T$. Wir können nun die Eigenschaft $f(a+b)=f(a)+f(b)$ nachprüfen:

$\def\arraystretch{1.25} \begin{array}{c l} f(a+b) &= f\left(\begin{pmatrix}a_x\\a_y\end{pmatrix}+\begin{pmatrix}b_x\\b_y\end{pmatrix}\right) \\ &= f\left(\begin{pmatrix}a_x + b_x\\a_y + b_y\end{pmatrix}\right) \\ &= \begin{pmatrix}\beta(a_x+b_x)\\a_y+b_y\end{pmatrix} \\ &= \begin{pmatrix}\beta a_x+\beta b_x\\a_y+b_y\end{pmatrix} \\ &= \begin{pmatrix}\beta a_x\\a_y\end{pmatrix}+\begin{pmatrix}\beta b_x\\b_y\end{pmatrix} \\ &= f\left(\begin{pmatrix}a_x\\a_y\end{pmatrix}\right)+f\left(\begin{pmatrix}b_x\\b_y\end{pmatrix}\right) \\ &= f(a)+f(b) \end{array}$

Schauen wir uns nun die Verträglichkeit mit der skalaren Multiplikation an. Die folgende Grafik zeigt, dass es egal ist, ob der Vektor $a$ zuerst mit einem Faktor $\lambda$ skaliert und dann in $x$-Richtung gestreckt wird oder zuerst in $x$-Richtung gestreckt und dann mit $\lambda$ skaliert wird:

Auch das lässt sich formal zeigen: Für $a\in\R^2$ und \lambda $\in\R$ gilt

$\def\arraystretch{1.25} \begin{array}{c l} f(\lambda a) &= f\left(\lambda \begin{pmatrix}a_x\\a_y\end{pmatrix} \right) = f\left(\begin{pmatrix}\lambda a_x\\\lambda a_y\end{pmatrix}\right) \\[0.5em] &= \begin{pmatrix} \beta (\lambda a_x)\\\lambda a_y\end{pmatrix} = \begin{pmatrix} \lambda\beta a_x\\\lambda a_y\end{pmatrix}\\[0.5em] &=\lambda \begin{pmatrix}\beta a_x\\a_y\end{pmatrix} = \lambda f\left(\begin{pmatrix}a_x\\a_y\end{pmatrix}\right)\\[0.5em] &= \lambda f(a). \end{array}$

Damit ist unser f eine lineare Abbildung.