Die (bedingte) Wahrscheinlichkeit von unter der Bedingung ist die Wahrscheinlichkeit, dass eintritt, falls sicher ist, dass schon eingetreten ist.
Man schreibt oder für die Wahrscheinlichkeit von unter der Bedingung .
(umgeformte erste Pfadregel)
wird gelesen als: "Wahrscheinlichkeit von unter der Bedingung "
Die bedingte Wahrscheinlichkeit ist nur sinnvoll definiert, wenn ist.
Beispiele und Abgrenzung von "normaler" Wahrscheinlichkeit
Die bedingte Wahrscheinlichkeit für "Die Straße ist nass, wenn es regnet" ist nahe 1 (Es gibt nur einige wenige Straßen, die überdacht sind.) Die Wahrscheinlichkeit für "Die Straße ist nass." (normale Wahrscheinlichkeit) ist deutlich unter 1 (je nach geographischer Lage).
Die bedingte Wahrscheinlichkeit für "lange Haare bei Frauen" ist deutlich höher als die Wahrscheinlichkeit für "lange Haare"
Ein Tetraeder (Zahlen 1-4) und ein Würfel (Zahlen 1-6) werden zufällig aus einer Urne gezogen und geworfen. Die Wahrscheinlichkeit für "1" berechnet man mit Die bedingte Wahrscheinlichkeit "1, wenn ich weiß, dass der Tetraeder gezogen wurde" berechnet man mit .
Ein ausführliches Beispiel

Ein Spielwürfel hat die Augenzahlen von bis , die bei einem Wurf alle die gleiche Wahrscheinlichkeit haben.
Wir nehmen jetzt zwei Ereignisse:

Ereignis : die geworfene Augenzahl ist durch drei teilbar, es ist also eine oder eine .
Bei sechs möglichen Fällen und zwei Fällen, in denen das Ereignis eintritt, ist die Wahrscheinlichkeit oder nach Kürzen .

Ereignis : die geworfene Augenzahl liegt zwischen und .
Da es sechs mögliche und vier Fälle, in denen das Ereignis eintritt, gibt, ist die Wahrscheinlichkeit oder nach Kürzen
Berechnung der bedingten Wahrscheinlichkeit: 1. Weg
Jetzt berechnen wir die Wahrscheinlichkeit von unter der Bedingung, dass auch eintritt. Das schreibt man als oder als .

Weil eintritt, ist die Grundmenge der möglichen Fälle jetzt nur noch .

Das Ereignis tritt ein bei einer oder einer , wobei die aber sicher ausgeschlossen ist.

Die einzige Möglichkeit, dass das Ereignis eintritt ist also, dass die geworfen wird.
Wir haben hier vier mögliche Fälle und nur einen, in dem das Ereignis eintritt. Das bedeutet, dass die bedingte Wahrscheinlichkeit von unter der Bedingung gleich ist: .
Berechnung der bedingten Wahrscheinlichkeit: 2. Weg
Dass die Ereignisse und beide eintreten, schreibt man als (eben dem Durchschnitt der Ereignismengen). Genau wie gerade sieht man, dass das einzige Ereignis ist. Die Wahrscheinlichkeit, eine zu werfen, ist (wie für jede einzelne Zahl) .
Daraus und aus kann man jetzt berechnen:
Wenn ist, muss diese Zahl mit multipliziert werden, damit auch das Ereignis eintritt. Dann sind aber beide Ereignisse und eingetreten, das heißt, man ist im Fall .
Man kann die Gleichung
nach auflösen und erhält
In diesem Beispiel ist
Zusammenfassung
Wenn man zwei der drei Wahrscheinlichkeiten , und kennt, kann man die dritte durch Umstellen der Formel berechnen:
Berechnung der bedingten Wahrscheinlichkeit von unter der Bedingung
Berechnung der Wahrscheinlichkeit, dass und beide eintreten
Berechnung der Wahrscheinlichkeit von
Aufgabe
Jetzt kannst du überprüfen, wie gut du das Beispiel verstanden hast: Berechne sowohl direkt als auch mit einer passenden Formel.
Häufige Fälle
Folgende Wahrscheinlichkeiten sind immer voneinander zu unterscheiden:
bezeichnet die Wahrscheinlichkeit von unter der Bedingung . d. h., man weiß bereits sicher, dass zutrifft bzw. eingetreten ist, aber bezüglich weiß man es nicht und fragt nach der Wahrscheinlichkeit von .
bezeichnet die Wahrscheinlichkeit von unter der Bedingung . d. h., man weiß bereits sicher, dass zutrifft bzw. eingetreten ist, aber bezüglich weiß man es nicht und fragt nach der Wahrscheinlichkeit von .
bezeichnet die Wahrscheinlichkeit des Ereignisses „ und zugleich “. d. h., man hat keine zusätzlichen Informationen und fragt nach der Wahrscheinlichkeit, mit der und gemeinsam eintreten.
Frage: Sei ein beliebiges Ereignis. Wie groß ist und ?
Schreib- und Sprechweisen
Man schreibt oder für die Wahrscheinlichkeit von unter der Bedingung .
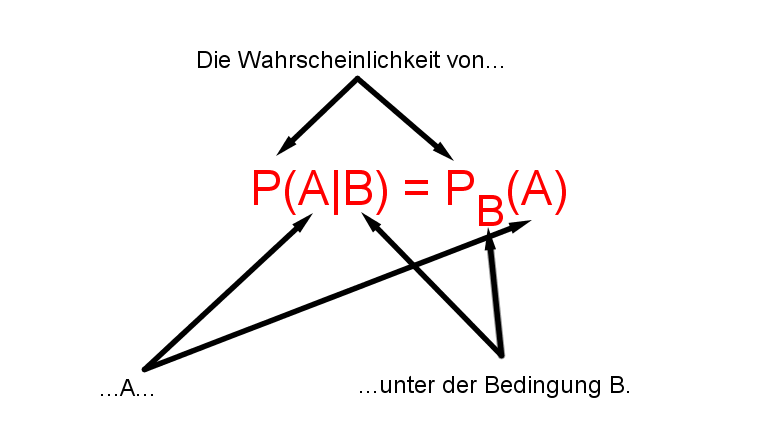
Alternative Sprechweisen:
„ unter der Bedingung “
„, wenn “
„Wahrscheinlichkeit von , wenn eingetreten ist“
„ gegeben “
Definition
Die bedingte Wahrscheinlichkeit ist wie folgt definiert:
Die bedingte Wahrscheinlichkeit am Baumdiagramm
Die bedingte Wahrscheinlichkeit kann ganz einfach am Baumdiagramm dargestellt werden:
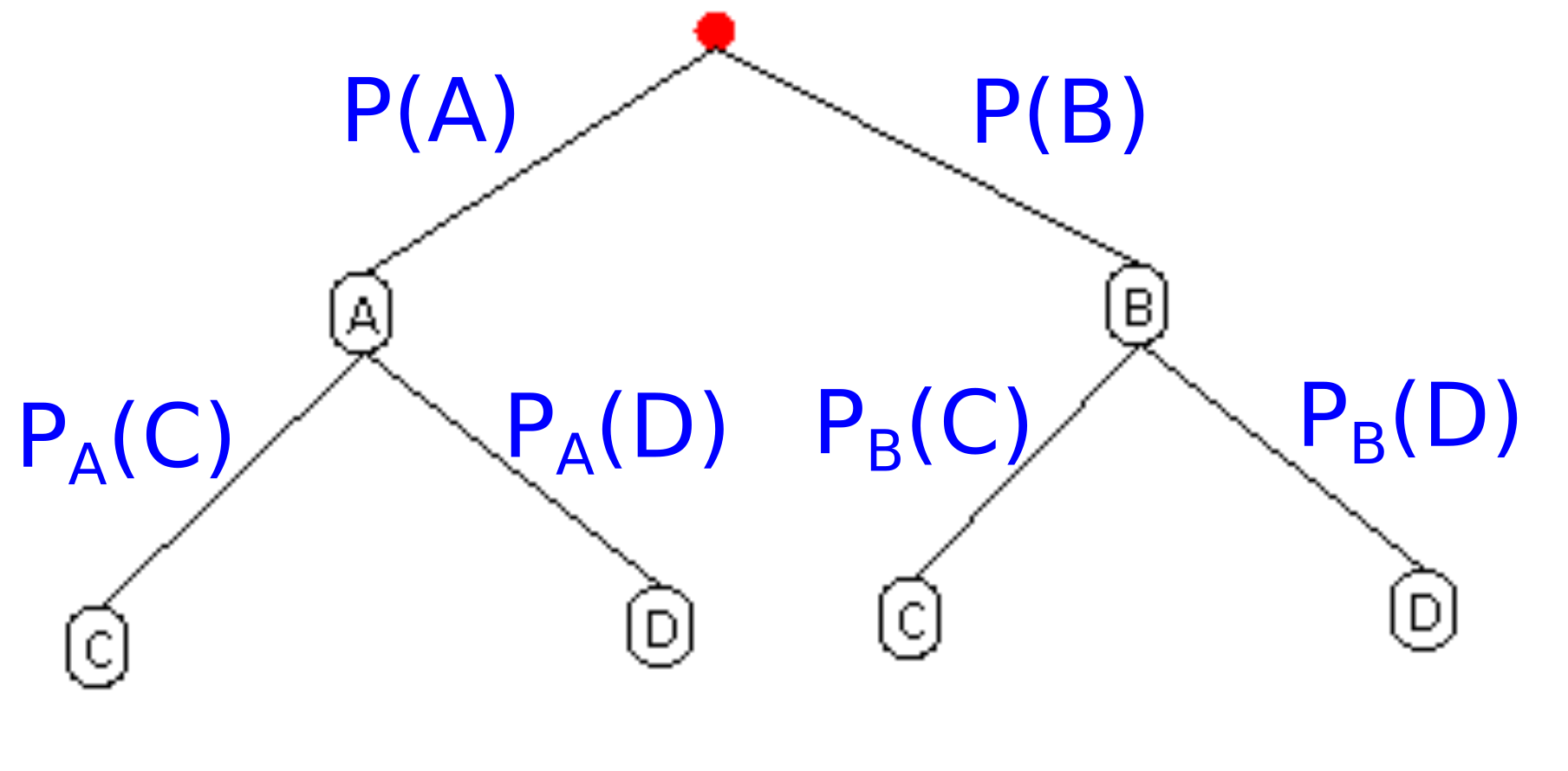
In einem zweistufigen Zufallsexperiment können in der ersten Stufe die Ereignisse und eintreffen, in der der zweiten Stufe die Ereignisse und .
Am dargestellten Baum kann man erkennen, dass die bedingten Wahrscheinlichkeiten in der zweiten Stufe zu finden sind. Sie hängen (bei Abhängigkeit) von der ersten Stufe ab.
Folgende Gleichungen gelten:
(erste Pfadregel)
(zweite Pfadregel)
Bedingte Wahrscheinlichkeit und Vierfeldertafel
Selbstverständlich kann man auch eine Vierfeldertafel erstellen, um alle Wahrscheinlichkeiten zu bekommen, die man benötigt, um auszurechnen. Beispielaufgabe mit ausführlicher Musterlösung
Bedingte Wahrscheinlichkeit und stochastische Unabhängigkeit
Weiß man, dass zwei Ereignisse stochastisch unabhängig sind, so vereinfacht sich zu . In diesem Fall ergibt sich für . Im Umkehrschluss: Unterscheiden sich und , so folgt, dass und stochastisch abhängig sind.
Wichtige Sätze
Aus der Definition und mithilfe der Pfadregeln lassen sich wichtige Sätze für die bedingte Wahrscheinlichkeit ableiten:
Multiplikationssatz
Gesetz der totalen Wahrscheinlichkeit
mit der Verallgemeinerung:
Satz von Bayes
Weiterer Satz
Beispiel:
Angenommen, ein bestimmtes Merkmal trete bei aller neugeborenen Mädchen und bei aller neugeborenen Jungen auf.
Folgende Ereignisse sollen betrachtet werden:
: „Das Kind hat das Merkmal .“
: „Das Kind ist ein Junge.“
Es soll davon ausgegangen werden, dass es gleich viel Jungen- wie Mädchengeburten gibt. Dann gilt:
, denn laut Angabe tritt Merkmal ja bei aller neugeborenen Jungen auf.
denn da nur der neugeborenen Kinder Jungen sind und unter den Jungen nur das Merkmal haben, ist die Wahrscheinlichkeit, dass ein beliebiges Kind ein Junge ist, der das Merkmal hat, gleich .
, denn das Merkmal betrifft Jungen viermal so oft wie Mädchen; wenn man also weiß, dass ein bestimmtes Kind das Merkmal hat, dann ist die Wahrscheinlichkeit , dass das Kind ein Junge ist.
