In der Kombinatorik interessiert man sich dafür, wie viele Möglichkeiten es für die Ergebnisse bestimmter Versuchsanordnungen gibt - z.B., um die Wahrscheinlichkeit für das Auftreten eines solchen Ereignisses zu berechnen.
Viele Probleme dieser Art lassen sich auf Urnenmodelle zurückführen.
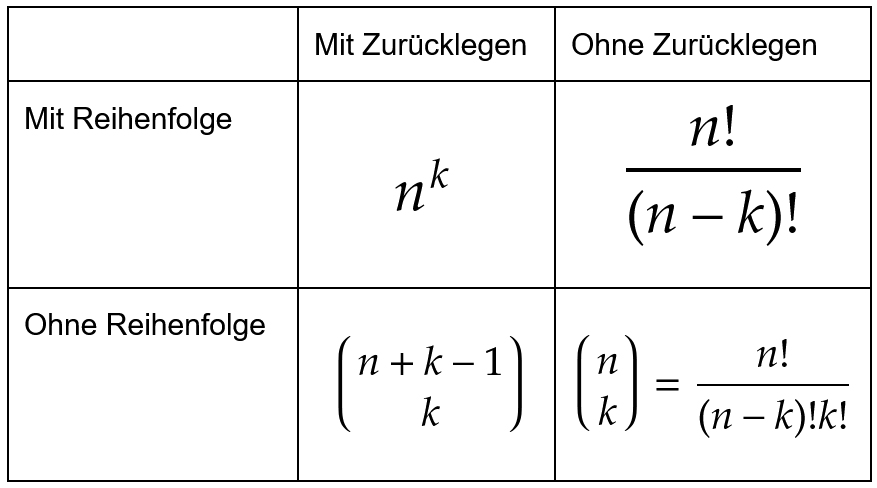
Einführung und Motivation
Wir stellen uns dazu unterscheidbare Kugeln (nummerierte Lottokugeln) in einer Urne vor, aus denen nun nacheinander Kugeln gezogen werden. Wenn Wahrscheinlichkeiten interessieren, soll bei jedem Zug die Wahrscheinlichkeit für jede Kugel gleich sein ("blind ziehen"), zum Anzählen der Möglichkeiten reicht es, wenn in jedem Zug jede Kugel drankommen kann. Im Folgenden seien , wobei wir setzen.
Für den Versuchsaufbau sind zwei Entscheidungen zu treffen:
man kann die gezogene Kugel wieder in die Urne zurücklegen (nachdem man sich die Nummer notiert hat…) oder nicht und
man kann sich beim Ergebnis dafür interessieren, in welcher Reihenfolge die Kugeln gezogen wurden oder nicht (letztes trifft z.B. beim Lotto zu, wo die Lottogesellschaft uns die Zahlen sortiert).
Somit sind vier verschiedene Fälle zu betrachten.
Ziehen mit Zurücklegen, mit Berücksichtigung der Reihenfolge
Wenn wir die Kugeln wieder zurückwerfen, haben wir in jedem der Züge Möglichkeiten.
Das ist also wie in der Aufgabe mit den möglichen Zuständen von Bit, nur dass dort der Spezialfall untersucht wurde.
Für allgemeines haben wir dann verschiedene Möglichkeiten.
Ziehen ohne Zurücklegen, mit Berücksichtigung der Reihenfolge
Jetzt werfen wir gezogene Kugeln nicht wieder zurück.
Dann haben wir im ersten Zug nach wie vor Kugeln, im zweiten Zug aber nur noch , im dritten , , im letzten (-ten) Zug noch Kugeln zur Auswahl.
Beim -ten der Züge also Möglichkeiten, also insgesamt
mögliche Ergebnisse.
Das lässt sich schreiben als
Wichtig ist hier der Spezialfall : es gibt Möglichkeiten, um Objekte anzuordnen.
Ziehen ohne Zurücklegen, ohne Berücksichtigung der Reihenfolge
Jetzt sortieren wir die Kugeln nach ihrer Nummerierung, bevor wir das Ergebnis verkünden - die Zugfolgen und zählen nun als gleich, wir sind also beim klassischen Lotto. Wie viele Möglichkeiten gibt es nun noch?
Wir haben vorhin gesehen, dass es bei Objekten verschiedene Anordnungen gibt. Daher müssen wir das vorherige Ergebnis einfach durch dividieren
Die Anzahl der verschiedenen Anordnungsmöglichkeiten ist also genau durch die Binomialkoeffizient gegeben.
Ziehen mit Zurücklegen, ohne Berücksichtigung der Reihenfolge
Der schwierigste Fall zuletzt: wir werfen die Kugeln in die Urne zurück und identifizieren Zugfolgen, die sich nur in der Reihenfolge unterscheiden, d.h., wir interessieren uns nur dafür, wie oft welche Kugel gezogen wird.
Zum Beweis ersetzen wir das ursprüngliche Modell mit Kugeln und Zellen durch ein anderes Modell:
Positionen. Verteile Striche auf diese Positionen. Alle Positionen ohne Strich erhalten (einen Stern).
Auf diese Art und Weise kann jedes mögliche Ereignis des ursprünglichen Urnenmodells eindeutig codiert werden.
Nun interpretieren wir dieses Strich-Modell wieder als ein Urnenmodell: Kugeln mögliche Positionen von . Gezogen werden Kugeln ohne Zurücklegen und ohne Berücksichtigung der Reihenfolge. Jede gezogene Kugel ist eine Position der Striche.
Daher gibt es
Möglichkeiten, nämlich so viele, wie es Möglichkeiten gibt, aus den Zahlen genau zu ziehen (ohne Zurücklegen und ohne Berücksichtigung der Reihenfolge).
