Gemischte Aufgaben zum Rechnen mit Brüchen
Hier findest du gemischte Rechenaufgaben und Textaufgaben, um das Rechnen mit Brüchen zu üben.
- 1
Berechne folgenden Term:
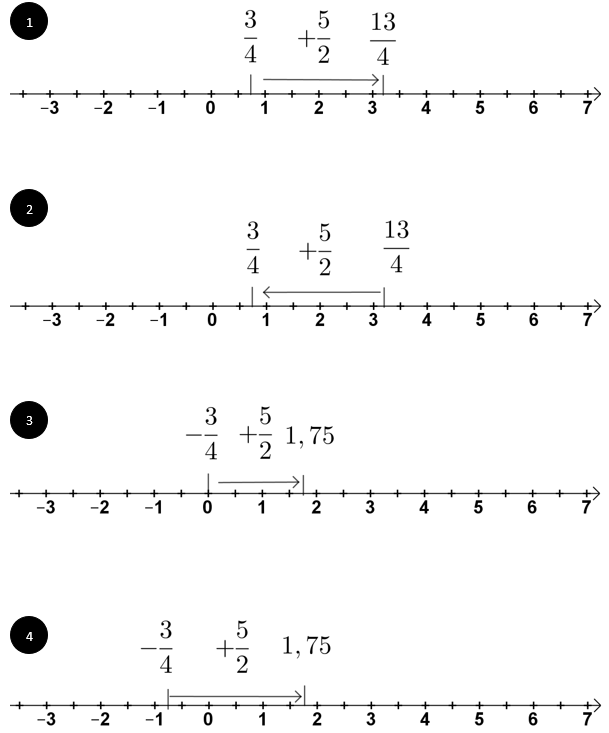
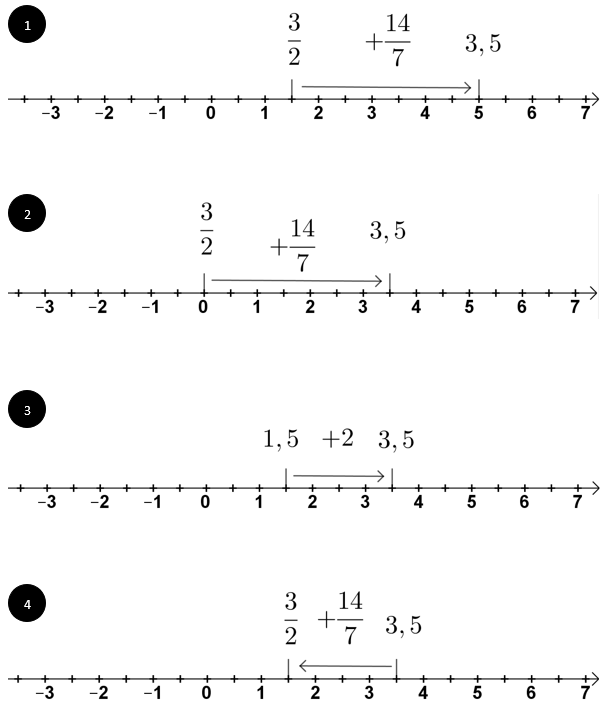
- 2
Bestimme die Lösung der Aufgabe mit Hilfe der Zahlengerade.
- 3
Welcher Graph entspricht der Rechenoperation? Trage die entsprechende Nummer in das Feld ein.
- 4
Berechne die folgenden Terme!
- 5
In Janas Klasse sind 30 Kinder, zwei Drittel davon können schwimmen.
Die Hälfte aller Schwimmer hat das silberne Schwimmabzeichen und zwei Fünftel sogar das goldene Schwimmabzeichen.
Wie viele Kinder können schwimmen?
Wie viele Kinder haben das silberne Schwimmabzeichen?
Wie viele Kinder haben das goldene Schwimmabzeichen?
Wie viele Kinder besitzen kein Schwimmabzeichen?
- 6
In der 6c sind der Schüler 11 Jahre alt und der Schüler 12 Jahre alt. 8 Schüler sind älter als 12 Jahre. Keines der Kinder ist jünger als 11 Jahre.
Welcher Anteil der Schüler ist älter als 12 Jahre?
Wie viele Schüler sind in der 6c?
- 7
Jana macht für ihre Geburtstagsfeier Zitronenlimo. Dafür schüttet sie 7 Flaschen Zitronensaft (je 0,5l Inhalt) und 9 Flaschen Mineralwasser (je 0,7l Inhalt) in einen 10l-Eimer.
Wie viel Liter Zitronenlimonade erhält sie?
Gib das Ergebnis als Dezimalzahl an.
Wie viel Liter passen noch in den Eimer?
Gib das Ergebnis als Dezimalzahl an.
Wie viele Gläser (350ml) lassen sich mit Janas Limo befüllen?
Jana möchte für jeden ihrer Gäste 2 Gläser Zitronenlimo bereitstellen.
Wie viele Gäste kann sie einladen?
- 8
Herr Huber behauptet: "Von meinem Monatslohn brauche ich ein Drittel für die Miete und ein Zehntel für mein Auto - da ist schon mehr als die Hälfte meines Einkommens weg."
Stimmt das?
- 9
Ein Multivitamin-Erfrischungsgetränk (500ml) besteht zur Hälfte aus Orangensaft, zu 25% aus Ananassaft, zu aus Zitronensaft. Dazu gibt man 20ml Limettensaft, der Rest wird mit Wasser aufgefüllt.
Wie viele ml Wasser benötigt man für den Drink?
- 10
In Max´ Familie gibt es jeden Tag Müsli zum Frühstück. Für eine Portion Müsli braucht man circa Milch und Haferflocken.
Neben Max und seinen Eltern wohnen auch seine zwei kleineren Geschwister und Oma Erna mit im Haus.
Wie viel Liter Milch braucht seine Familie pro Tag?
Wie viel kg Haferflocken braucht seine Familie pro Tag?
Max´ Mutter kauft im Großmarkt einen 5kg Maxi-Packung Haferflocken. Reicht diese Menge für eine Woche?
Sie kauft außerdem eine Palette Milch mit 12 Milchkartons zu je 1l.
Reicht das für für eine Woche?
- 11
Ein Grundstück ist 91m lang. Die Breite beträgt aber nur der Länge.
Wie viele Meter ist das Grundstück breit?
- 12
Während des Sportunterrichts läuft Jan km in 15min und Tim km in 21min. Wer ist schneller? Begründe deine Antwort
- 13
Aus Rindfleisch werden 18 gleich große Steaks geschnitten.
Wie viel Gramm wiegt ein Steak?
Herr Huber kauft für einen Grillabend 6 solcher Steaks.
Im Supermarkt sind diese gerade für 17€/kg im Angebot.
Wie viel kosten die Steaks von Herrn Huber?
(Eingabe in €)
Herr Huber will auch noch Grillwürste für seine Party kaufen.
Insgesamt hat er 30€ dabei.
Von diesem Geld bezahlt er zuerst die Steaks. Wie viele Würste kann er mit dem verbleibenden Geld noch kaufen?
Eine Wurst kostet 75ct.
- 14
Tim bekommt Besuch von seinen drei Freunden. Gemeinsam wollen sie Saft trinken.
Berechne, wie viel Saft jeder der (vier) Personen bekommt, wenn jeder genau gleich viel bekommt.
Einer von Tims Gästen ist leider krank. Deshalb wird sein Anteil nun unter allen Anwesenden fair aufgeteilt.
Wie viel Saft bekommt jeder Gast zusätzlich? [in ml]
- 15
Löse die Aufgaben.
Trenne im Eingabefeld Zähler und Nenner mit einem "/". Beispiel: Zähler/Nenner: 1/2.
Berechne den Wert der Differenz der Zahlen und .
Berechne den Wert der Differenz aus der Zahl 1 und dem Wert der Summe der Zahlen und .
Ermittle, um wie viel größer ist als der Wert der Differenz von und
Subtrahiere vom Produkt aus und
Dividiere die Differenz aus und durch .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?