Zwei Größen sind dann direkt proportional zueinander, wenn die eine Größe aus der anderen hervorgeht, indem man sie mit immer dem gleichen Faktor multipliziert.
Anders ausgedrückt: Bei der direkten Proportionalität zweier Größen ist das Verhältnis dieser Größen - also ihr Quotient - immer gleich. Das ist genau wie bei einem Bruch, dessen Wert sich nicht ändert, wenn man ihn kürzt oder erweitert.
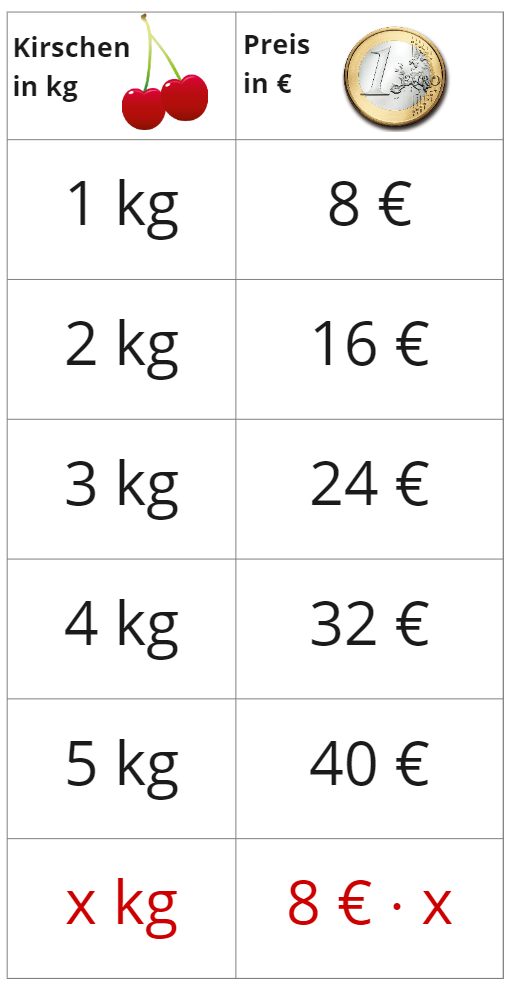
Für je ein Kilogramm Kirschen zahlst du in einem Laden . Der Zusammenhang zwischen Preis und Gewicht der Kirschen ist direkt proportional.
Kilogramm kosten .
Kilogramm kosten .
Kilogramm kosten .
...
Kilogramm kosten .
Um auf den Preis zu kommen, multiplizierst du das Gewicht der Kirschen, immer mit der gleichen Zahl - dem Preis für je ein Kilo Kirschen.
Darstellung
Die direkte Proportionalität wird mit dem Zeichen verdeutlicht.
bedeutet also " ist direkt proportional zu ".
Gewicht der Kirschen Preis der Kirschen
Begrifflichkeit
Größe 1 ist die Grundgröße, Größe 2 die zugeordnete Größe.
Das Verhältnis, in dem die beiden Größen zueinander stehen, wird auch Proportionalitätsfaktor oder Proportionalitätskonstante genannt.
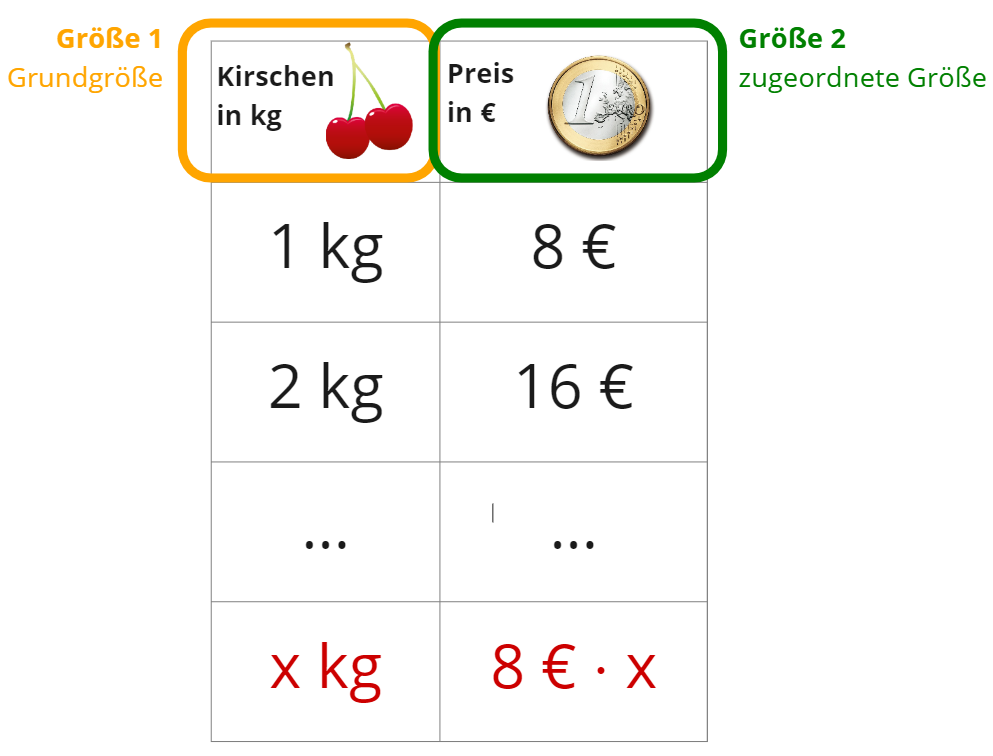
Im obigen Beispiel ist das Gewicht der Kirschen die und der Preis der Kirschen die .
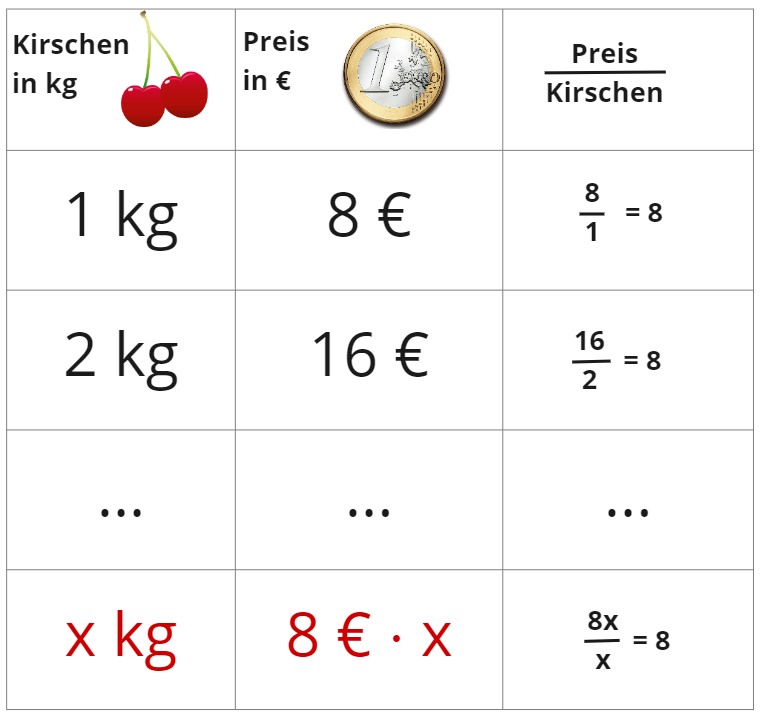
Der Preis ist proportional zum Gewicht. Die Proportionalitätskonstante ergibt sich aus dem Verhältnis der Grundgröße und der zugeordneten Größe. Hier ist die Proportionalitätskonstante .
Möchte man wissen, wie viel 10 Kilo Kirschen kosten, multipliziert du das Gewicht mit dem Proportionalitätsfaktor:
10 Kilo Kirschen kosten 80 €.
Der Funktionsgraph einer direkten Proportionalität
Trägt man alle berechneten Werte so in ein Koordinatensystem ein, dass auf der -Achse die Werte der Grundgröße und auf der -Achse die Werte der zugeordneten Größe stehen, dann ergibt sich immer eine Ursprungsgerade mit der Formel . Dabei ist der Proportionalitätsfaktor, welcher zugleich die Geradensteigung angibt.

Aus dem obigen Beispiel ergibt sich so ein Koordinatensystem, bei dem auf der x-Achse die Menge an Kirschen in kg steht. Die y-Achse beschreibt den Preis.
Die Funktionsgleichung der Zuordnung ist:
Eine mögliche Wertetabelle könnte sein:
1 | 2 | 3 | 4 | 5 | 6 | |
8 | 16 | 24 | 32 | 40 | 48 |
Video zum Thema direkte Proportionalität
Übungsaufgaben
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur direkten Proportionalität
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
