In diesem Artikel wird erklärt wozu wir den Lagrange-Formalismus benötigen.
In diesem Abschnitt werden wir den Lagrange-Formalismus kennenlernen, welcher die uns vertraute Newtonsche Mechanik auf beliebige Koordinaten verallgemeinert. Es ist eine weitere Formulierung der klassischen Mechanik, d.h. sie enthält keine neue Physik, ist aber zur Newtonschen Mechanik vollständig äquivalent und hilft uns dabei bestimmte physikalische Probleme einfacher zu lösen.
Der Lagrange-Formalismus findet zudem Anwendung in klassischen Feldtheorien und der Quantenmechanik / Quantenfeldtheorie, es lohnt sich also nicht nur für die klassische Mechanik sich damit zu beschäftigen.
Ausgangspunkt: Newtonsche Axiome
Von den Newtonschen Axiomen kennen wir die Bewegungsgleichungen (für konstante Massen)
Sie gelten in dieser Form jedoch nur für kartesische Koordinaten und in Inertialsystemen. Das kann unpraktisch sein, beispielsweise wenn die Koordinaten voneinander abhängig sind (also Zwangsbedingungen vorliegen) oder andere Koordinaten geschickter sind, um z.B. Symmetrien des Systems auszunutzen.
Natürlich kann man die Bewegungsgleichungen in andere Koordinaten transformieren, was jedoch sehr aufwändig sein kann. Wäre es nicht viel schöner die Bewegungsgleichungen direkt in anderen Koordinaten aufschreiben zu können? Genau das ermöglicht der Lagrange-Formalismus durch die Einführung sogenannter generalisierter Koordinaten, indem er die Newtonsche Mechanik auf beliebige Koordinaten verallgemeinert.
Beispiel: Ebenes Pendel in kartesischen Koordinaten
Als Beispiel wollen wir die Bewegungsgleichungen für ein Pendel aufstellen, welches unter dem Einfluss der Schwerkraft
in der -Ebene schwingt und im Koordinatenursprung aufgehängt ist (siehe Abb. 1). Dabei werden wir bewusst kartesische Koordinaten verwenden, um zu demonstrieren, wie die Wahl von Koordinaten den Lösungsweg beeinflusst.
Da die Länge des (masselosen!) Pendelfadens konstant ist, schränkt dieser die Bewegung ein durch die Bedingung
welche sich aus dem Satz des Pythagoras ergibt. Die Einhaltung dieser Zwangsbedingung wird sichergestellt durch die Zwangskraft , welche entlang des Pendelfadens wirkt und ebenfalls in den Newtoschen Bewegungsgleichungen berücksichtigt werden muss
Wir erhalten dadurch zwei Differentialgleichungen, in denen die Komponenten der Zwangskraft als weitere Unbekannte neben den Koordinaten und des Pendels auftreten
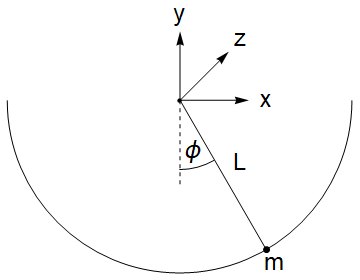
Abb. 1: Skizze eines ebenen Pendels in drei Dimensionen. Die Aufhängung schränkt die Bewegung des Pendelkörpers auf eine Kreisbahn mit Radius in der -Ebene ein.
Als nächstes berechnen wir explizit die Zwangskräfte und . Dabei helfen uns geometrische Überlegungen. Ein Blick auf Abb. 1 zeigt, dass wir die Pendelkoordinaten und durch den Winkel zwischen dem Pendel und der y-Achse ausdrücken können
Zudem stehen die beiden Komponenten der Zwangskraft und im selben Verhältnis zueinander, wie und
Damit tritt nur noch eine Komponente der Zwangskraft als Unbekannte auf. Um diese zu berechnen schauen wir uns nochmals die Zwangsbedingung an
und differenzieren diese zwei Mal nach der Zeit. Daraus folgt die Gleichung
in die wir die beiden Bewegungsgleichungen einsetzen
Ein wenig Umstellen und Multiplikation mit ergibt
Damit können wir die Zwangskraft explizit berechnen
und in die obigen Bewegungsgleichungen einsetzen, sodass wir ein gekoppeltes Differentialgleichungssystem erhalten
Diese Differentialgleichungen sind nicht besonders angenehm zu lösen. Schon während ihrer Herleitung hatten wir geometrische Überlegungen und den Winkel ausgenutzt, es ist daher naheliegend auch zur Parametrisierung der Bewegungsgleichung zu verwenden. Dadurch lässt sich eine wesentlich einfachere Bewegunsgleichung für das Pendel aufstellen.
Darüber hinaus bietet die Lagrange-Mechanik die Möglichkeit, die Berechnung von Zwangskräften und damit einhergehende komplexe geometrische Überlegungen zu umgehen, und so den Lösungsweg zur Bestimmung der Bewegungsgleichungen weiter zu vereinfachen.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
