1.0 Gegeben ist das Drachenviereck $ABCD$ mit der Symmetrieachse $BD$ und dem Diagonalenschnittpunkt $M$.

Es gilt: $\overline{AM}=\overline{DM}=2\ \text{cm}$ und $\overline{BD} = 6 \ \text{cm}$.

Punkte $E_n$ auf der Strecke $[BM]$ legen zusammen mit den Punkten $A, C$ und die Drachenvierecke $AE_nCD$ fest.

Die Winkel $CE_nA$ haben das Maß $\varphi$ mit $\varphi\in\lbrack53{,}13^\circ;\;180^\circ\lbrack.$

Die Zeichnung zeigt das Drachenviereck $ABCD$ und das Drachenviereck $AE_1CD$ für $\varphi=100^\circ$.

Runden Sie im Folgenden auf zwei Stellen nach dem Komma.

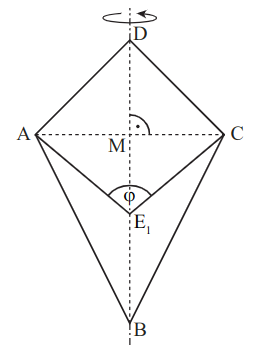
1.1 Zeichnen Sie das Drachenviereck $AE_2CD$ für $\varphi=70^\circ$ in die Zeichnung zu 1.0 ein. Bestätigen Sie sodann die untere Intervallgrenze für $φ$ durch Rechnung.

1.2 Die Drachenvierecke $AE_nCD$ rotieren um die Gerade $BD$. Zeigen Sie, dass für das Volumen $V$ der entstehenden Rotationskörper in Abhängigkeit von $\varphi$ gilt:

$V(\varphi)=\dfrac83\cdot\mathrm\pi\cdot(1+\frac1{\tan\left(0{,}5\cdot\mathrm\varphi\right)}\mathrm)\ \text{cm}^3$

1.3 Das Drachenviereck $AE_3CD$ ist ein Quadrat. Bestimmen Sie das Volumen des zugehörigen Rotationskörpers.