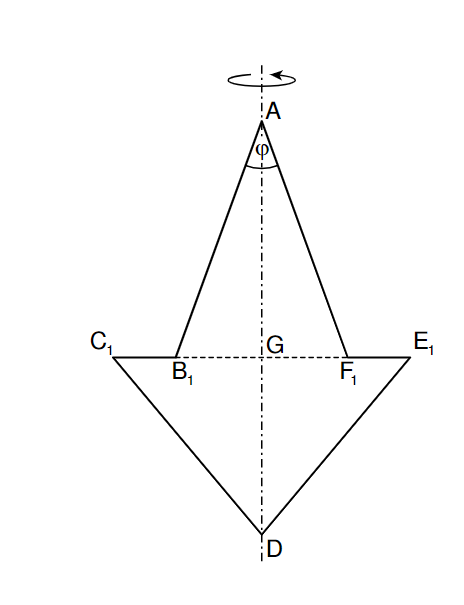
2.0 Gegeben sind Sechsecke $AB_nC_nDE_nF_n$ mit der Symmetrieachse $AD$. Der Punkt $G$ ist der Mittelpunkt der Strecken $[C_nE_n]$ und $[B_nF_n]$.

Es gilt: $\overline{AG}=4\;\text{cm}$ und $\overline{DG}=3\;\text{cm}$.

Die Winkel $B_nAF_n$ haben das Maß $\varphi$ und die Winkel $E_nDC_n$ haben das Maß $2\varphi$ mit $\varphi\in\,]0^\circ;\;90^\circ\lbrack.$

Die Zeichnung zeigt das Sechseck $AB_1C_1DE_1F_1$ für $\varphi= 40^\circ$.

2.1 Zeigen Sie, dass für die Längen der Strecken $[B_nF_n]$ und $[C_nE_n]$ in Abhängigkeit von $\varphi$ gilt: $\overline{B_nF_n}(\varphi)=8\cdot \textrm{tan}(0{,}5\cdot\varphi)\,\textrm{cm}$ und $\overline{C_nE_n}(\varphi)=6\cdot \textrm{tan}\varphi \ \textrm{cm}.$

2.2 Die Sechsecke $AB_nC_nDE_nF_n$ rotieren um die Gerade $AD$.

Zeigen Sie, dass für den Oberflächeninhalt $O$ der entstehenden Rotationskörper in Abhängigkeit von $\varphi$ gilt:

$O(\varphi)=\bigg(16\pi\cdot \frac{{\tan(0{,}5\cdot\varphi})}{\cos(0{,}5\cdot\varphi)}+9 \pi\cdot\frac{{\tan(\varphi})}{\cos(\varphi)}+9\pi\cdot \tan^2\varphi-16\pi\cdot \tan^2(0{,}5\cdot\varphi)\bigg)\ \text{cm}^2$.

2.3 Für das Sechseck $AB_2C_2DE_2F_2$ gilt: $\overline{AB_2}=\overline{B_2F_2}=\overline{F_2A}$.

Zeichnen Sie das Sechseck $AB_2C_2DE_2F_2$ in die Zeichnung zu 2.0 ein.

Berechnen Sie sodann den Oberflächeninhalt des zugehörigen Rotationskörpers. Runden Sie auf zwei Nachkommastellen.