Zwei Vektoren
Zwei Vektoren und nennt man linear abhängig, wenn der eine Vektor ein Vielfaches des anderen ist:
oder
Ist das nicht der Fall, dann nennen wir die Vektoren linear unabhängig.
Bildlich kann man sich das so vorstellen:
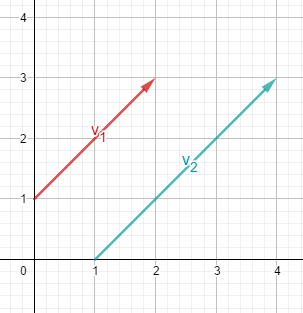
Linear abhängig: Die Vektoren sind "parallel" (Sie müssen dafür nicht in die selbe Richtung zeigen, sondern können auch in genau entgegengesetzte Richtungen zeigen!)
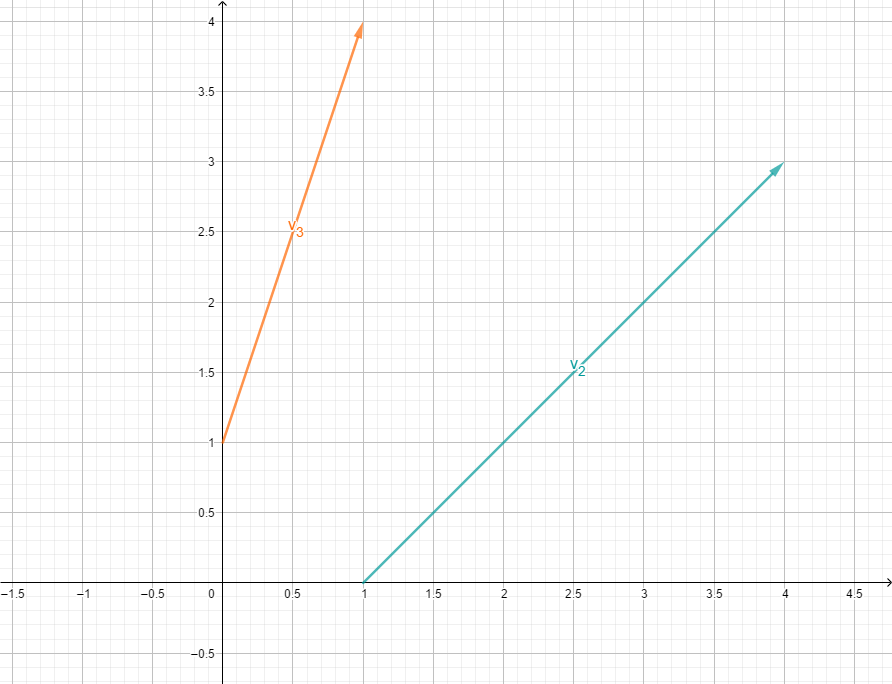
Linear unabhängig: Die Vektoren sind "nicht parallel"
Beispiel 1
Geben sind folgende Vektoren:
und
Jetzt versuchen wir eine passende Zahl n zu finden, mit der wir multiplizieren, damit rauskommt.
Wenn wir die x-Koordinate von mit 3 multiplizieren, erhalten wir die passende x-Koordinate von .
Jetzt prüfen wir noch, ob dies auch für die - und -Koordinaten gilt:
-Koordinate:
-Koordinate:
Wir stellen fest: stimmt! Also sind die beiden Vektoren linear abhängig.
Beispiel 2
Gegeben sind folgende Vektoren:
und
Wir versuchen wieder eine passende Zahl n zu finden, mit der ein Vielfaches von ist. Dafür gehen wir wieder Koordinatenweise vor:
Die x-Koordinate von erhalten wir, indem wir die -Koordinate von mit multiplizieren.
Dies gilt auch für die -Koordinate:
Dies gilt aber nicht für die -Koordinate:
Somit konnten wir keine passende Zahl finden und daher sind und linear unabhängig.
