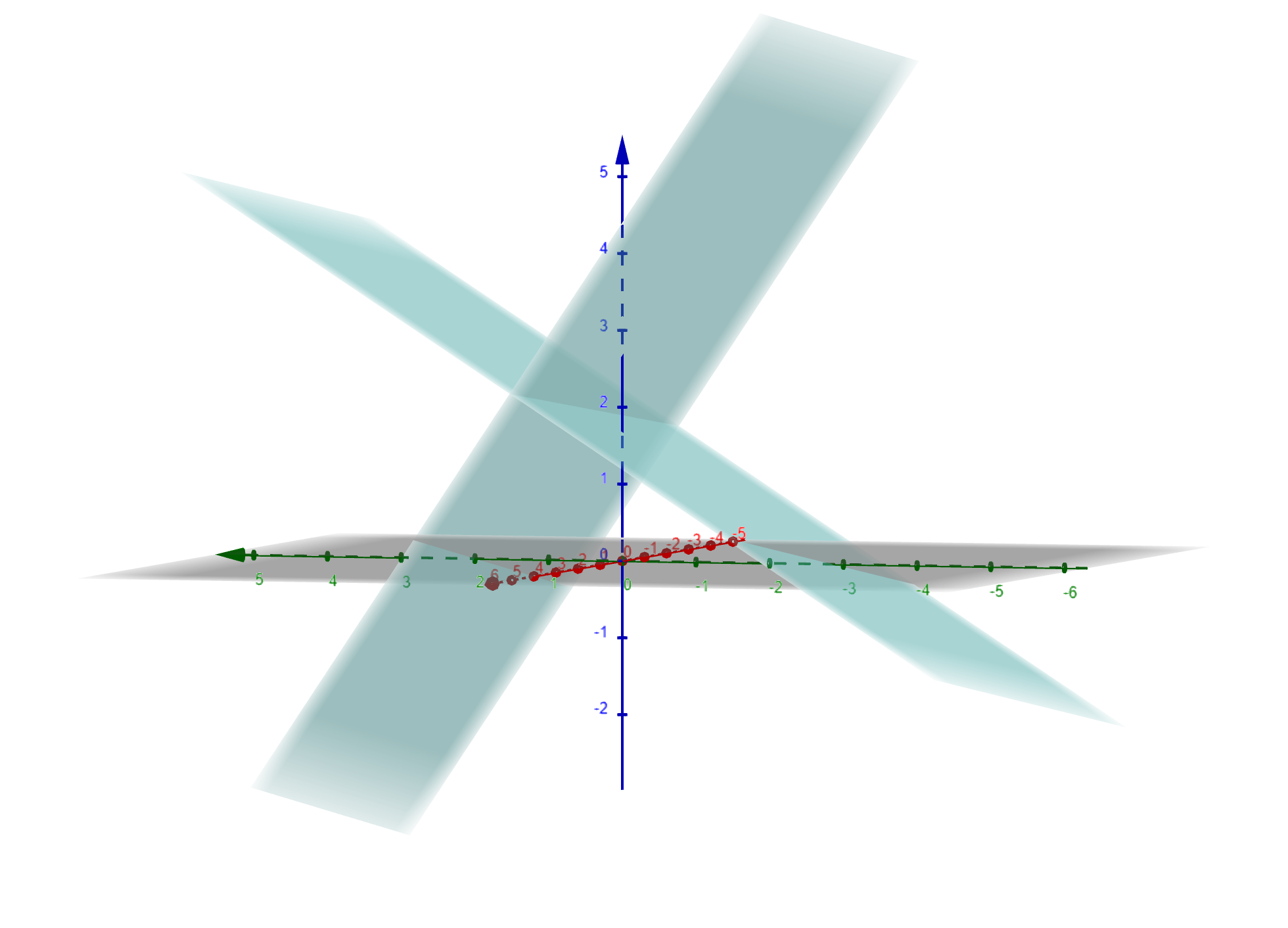
Zwei Ebenen können sich in verschiedenen Lagen zueinander befinden. Sie können bspw. senkrecht aufeinander stehen, siehe Abbildung.
Das bedeutet nicht, dass jeder Vektor der ersten Ebene senkrecht auf einem Vektor der zweiten Ebene steht.
Sie schneiden sich zwangsläufig in einer Schnittgerade.
Wie man bestimmt, ob zwei Ebenen aufeinander senkrecht stehen hängt von der Form ab, in der sie gegeben sind.
Normalform Sind zwei Ebenen in der Normalform gegeben, dann stehen sie aufeinander senkrecht , wenn ihre Normalvektoren aufeinander senkrecht stehen (siehe " Bei Vektoren "):
E 1 : n ⃗ 1 ∘ x ⃗ = a 1 ( a 1 ∈ R ) E 2 : n ⃗ 2 ∘ x ⃗ = a 2 ( a 2 ∈ R ) E 1 ⊥ E 2 ⇔ n ⃗ 1 ∘ n ⃗ 2 = 0 \def\arraystretch{1.25} \begin{array}{l}E_1:\;{\vec n}_1\circ\vec x=a_1\;\;\;\;\;\;\;(a_1\in ℝ)\\E_2:\;{\vec n}_2\circ\vec x=a_2\;\;\;\;\;\;\;(a_2\in ℝ)\\\\E_1\perp E_2\Leftrightarrow{\vec n}_1\circ{\vec n}_2=0\end{array} E 1 : n 1 ∘ x = a 1 ( a 1 ∈ R ) E 2 : n 2 ∘ x = a 2 ( a 2 ∈ R ) E 1 ⊥ E 2 ⇔ n 1 ∘ n 2 = 0
Beispiel Die Ebenen E 1 : − 2 x 1 + x 2 + 3 x 3 = − 4 E 2 : x 1 − x 2 + x 3 = 1 \def\arraystretch{1.25} \begin{array}{l l} E_1&:& -2&x_1&+&x_2&+3&x_3&&=&-4\\
E_2&:&&x_1&-&x_2&+&x_3&&=&1
\end{array} E 1 E 2 : : − 2 x 1 x 1 + − x 2 x 2 + 3 + x 3 x 3 = = − 4 1
besitzen die Normalenvektoren:
n 1 = ( − 2 1 3 ) , n 2 = ( 1 − 1 1 ) \displaystyle \def\arraystretch{1.25} n_1=\left(\begin{array}{l} -2\\
1\\
3
\end{array}\right),
n_2=\left(\begin{array}{l} 1\\
-1\\
1
\end{array}\right) n 1 = − 2 1 3 , n 2 = 1 − 1 1 Da ihr Skalarprodukt 0 0 0 E 1 , E 2 E_1,E_2 E 1 , E 2
Schreibe E 1 ⊥ E 2 E_1\perp E_2 E 1 ⊥ E 2
Parameterform Sind die Ebenen in der Parameterform gegeben, so ist es am einfachsten, mithilfe des Kreuzproduktes der beiden Richtungsvektoren die Normalvektoren zu bestimmen. Die können wie im oberen Beispiel auf Orthogonalität überprüft werden:
E 1 : x ⃗ = r ⃗ 1 + λ a ⃗ 1 + μ b ⃗ 1 E 2 : x ⃗ = r ⃗ 2 + λ a ⃗ 2 + μ b ⃗ 2 ( λ , μ ∈ R ; a ⃗ 1 , a ⃗ 2 , b ⃗ 1 , b ⃗ 2 ≠ 0 ⃗ ) E 1 ⊥ E 2 ⇔ ( a ⃗ 1 × b ⃗ 1 ) ∘ ( a ⃗ 2 × b ⃗ 2 ) = 0 \def\arraystretch{1.25} \begin{array}{l}E_1:\vec x={\vec r}_1+\lambda{\vec a}_1+\mu{\vec b}_1\\E_2:\vec x={\vec r}_2+\lambda{\vec a}_2+\mu{\vec b}_2\;\;\;\;\;\;(\lambda,\mu\;\in ℝ;\;\;{\vec a}_1,{\vec a}_2,{\vec b}_1,{\vec b}_2\neq\vec0)\\\\E_1\perp E_2\Leftrightarrow({\vec a}_1\times{\vec b}_1)\circ({\vec a}_2\times{\vec b}_2)=0\end{array} E 1 : x = r 1 + λ a 1 + μ b 1 E 2 : x = r 2 + λ a 2 + μ b 2 ( λ , μ ∈ R ; a 1 , a 2 , b 1 , b 2 = 0 ) E 1 ⊥ E 2 ⇔ ( a 1 × b 1 ) ∘ ( a 2 × b 2 ) = 0
Übungsaufgaben: Zwei zueinander senkrechte Ebenen Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:Aufgaben zur Lagebeziehung zweier Ebenen
Du hast noch nicht genug vom Thema? Hier findest du noch weitere passende Inhalte zum Thema:
Artikel 
