Geometrisches Mittel

Das geometrische Mittel ist ein Mittelwert der Statistik. Es ist immer kleiner oder gleich dem arithmetischen Mittel.

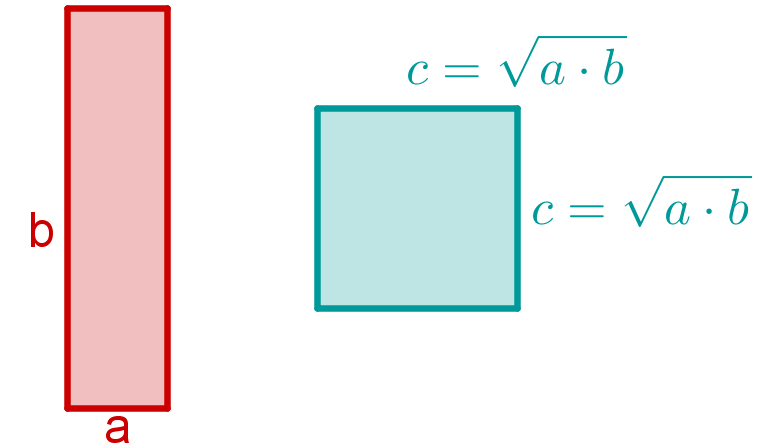
Geometrisches Mittel c von a und b

Formel

Um das geometrische Mittel von $n$ Zahlen $x_{1}, x_{2}, \dots, x_{n}$ zu ermitteln, muss man deren Produkt bilden und von diesem die $n$ -te Wurzel ziehen.

Damit ergibt sich die Formel:

$G (x_{1}, x_{2}, \dots, x_{n}) = x_{geom} = {\sqrt[n]{x_{1} \cdot x_{2} \dots x}}_{n} = \sqrt[n]{\prod_{i = 1}^{n} x_{i}}$ .

Wichtig

Keiner der Werte darf negativ sein. Sonst steht möglicherweise etwas Negatives unter der Wurzel stehen.
Keiner der Werte darf $0$ sein. Sonst wäre das Ergebnis auch $0$ .

Geometrische Interpretation

Berechnet man das geometrische Mittel zweier Zahlen $a$ und $b$ , $G (a, b) = x_{geom} = \sqrt[2]{a \cdot b} = \sqrt{a \cdot b}$ , so kann man das geometrische Mittel als die Seitenlänge $c$ eines Quadrats interpretieren, welches den gleichen Flächeninhalt wie das Rechteck mit den Seitenlängen $a$ und $b$ hat.

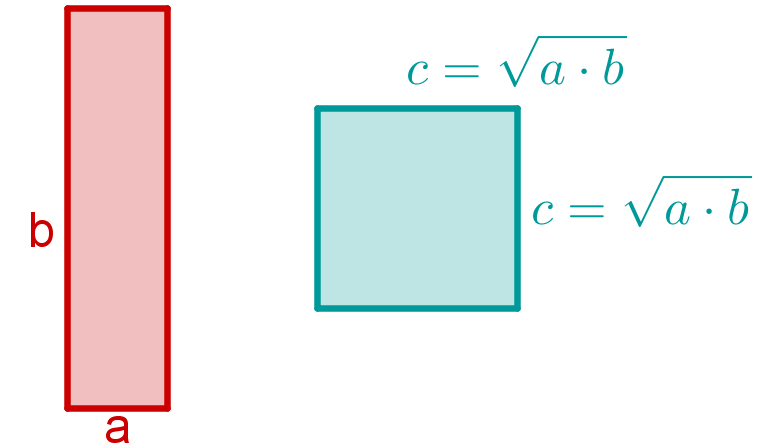
Anwendung

Gerade für die Finanzmathematik ist das geometrische Mittel wichtig, da man mit ihm durchschnittliche Wachstumsfaktoren, wie zum Beispiel das BIP-Wachstum oder das durchschnittliche Wachstum der Unternehmensgewinne, berechnet werden können.

Beispiel 1

Laden

Beispiel 2 mit Herleitung

Laden

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?