Das Kommutativgesetz oder Vertauschungsgesetz gilt dann, wenn man die einzelnen Elemente in ihrer Reihenfolge vertauschen kann, ohne dass sich am Ergebnis etwas ändert.
Das Kommutativgesetz ist erfüllt bei der Addition und der Multiplikation, nicht aber bei der Subtraktion und der Division.
Kommutativgesetz der Addition
Auf die Addition angewendet besagt das Kommutativgesetz:
Man sagt auch: "Die Addition ist kommutativ."
Rechenbeispiele
und | |
mit negativen Zahlen | und |
mit positiven und negativen Zahlen | und |
mit Brüchen |
Das Kommutativgesetz der Addition gilt nicht nur beim Rechnen mit Zahlen, sondern auch beim Rechnen mit Variablen:
Kommutativgesetz der Addition im Alltag
Das Kommutativgesetz der Addition ist von der alltäglichen Erfahrung her vertraut und selbstverständlich:
Wenn man zum Beispiel in eine Tüte erst drei Äpfel hineinlegt, und danach noch zwei weitere Äpfel hinzufügt, sind in der Tüte natürlich genauso viele Äpfel, als wie wenn man erst die zwei Äpfel hineingelegt und danach die drei Äpfel hinzugefügt hätte.
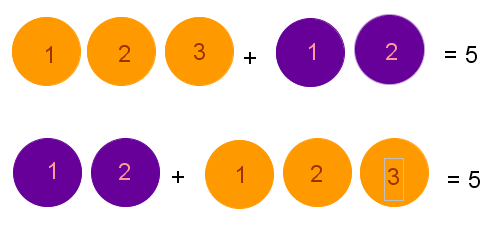
Kommutativgesetz der Multiplikation
Auf die Multiplikation angewendet besagt das Kommutativgesetz:
In einem Produkt kann man die Faktoren in ihrer Reihenfolge beliebig vertauschen, ohne dass sich der Wert des Produkts ändert.
Man sagt auch: "Die Multiplikation ist kommutativ."
Rechenbeispiele
und ebenso | |
mit negativen Zahlen | und |
Ein Schüler soll die Fläche eines Papierblattes berechnen. Das Blatt ist lang und breit. Die Formel für die Fläche ist: . Nach dem Kommutativgesetz kann der Schüler aber auch benutzen und das Ergebnis bleibt gleich.
Kommutativ-, Assoziativ- und Distributivgesetz im Video
In diesem Video wird unter anderem das Kommutativgesetz erklärt und mit Hilfe von Beispielen vertieft.
Laden
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Addition und Subtraktion ganzer Zahlen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
