Flächeninhalt eines Dreiecks

Von inyono 20.11.2018, 11:55:19

Titel

Flächeninhalt eines Dreiecks

Inhalt 🟠

Um die Fläche eines Dreiecks zu berechnen, gibt es grundsätzlich mehrere Möglichkeiten:

1.- Berechnung mit Grundlinie und zugehöriger Höhe

allgemein
Sonderfälle für rechtwinkliges und für gleichseitiges Dreieck

\displaystyle A_{\Delta}=\frac{1}{2}\cdot g \cdot h

2.- Berechnung mit zwei Seiten und dem Sinus des Winkels dazwischen

\displaystyle A_{\Delta}=\frac{1}{2}\cdot a \cdot b \cdot \sin \gamma

3.- Berechnung mit einer Determinante (nur im Koordinatensystem möglich)

\displaystyle A_{\Delta}=\frac{1}{2}\cdot |\vec{AB}\times\vec{AC}|

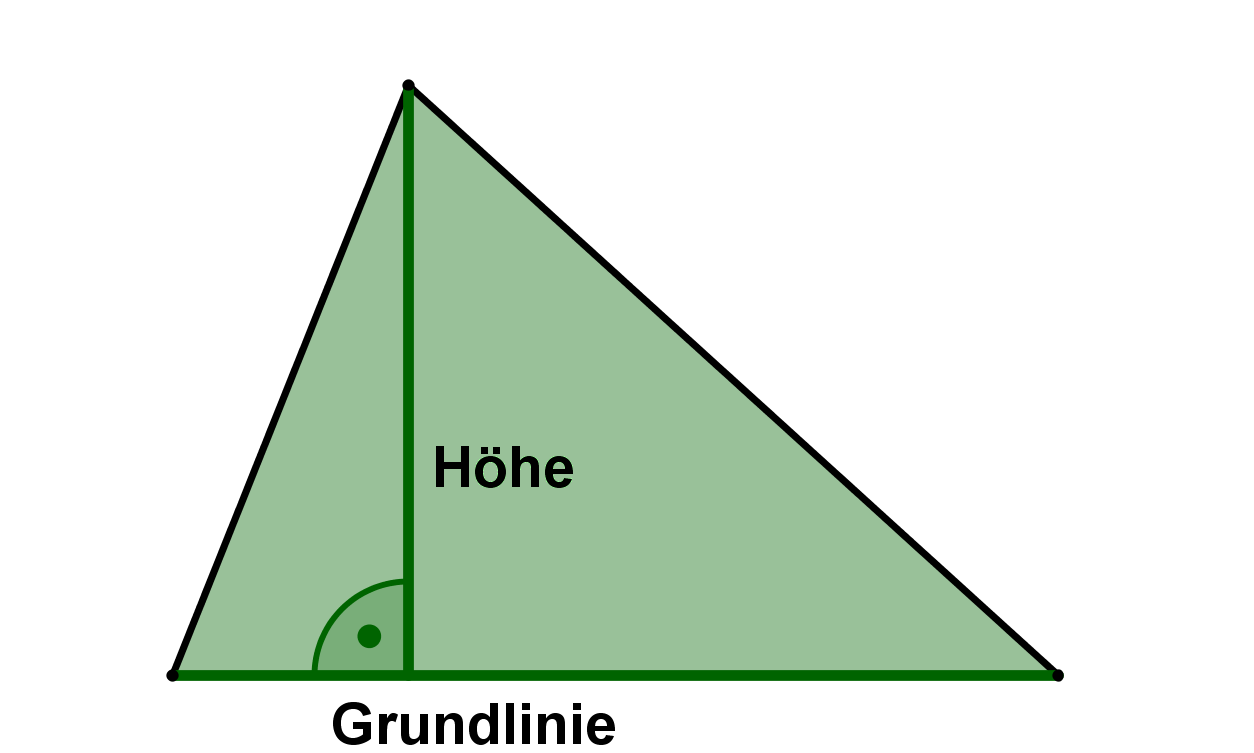
Dreiecksfläche mit Grundlinie und Höhe berechnen

Dies ist die zumeist verwendete Methode. Man braucht dabei zur Berechnung der Dreiecksfläche $A_{\Delta}$

die Grundlinie $g$ und
die Höhe $h$ des Dreiecks.

Die Formel lautet:

\displaystyle A_{\Delta}=\frac{1}{2}\cdot g \cdot h

Alt: Graphik zur Veranschaulichung von Grundlinie und HöheLink: (kein Link)

Verschiedene Versionen der Formel

Grundlinie $g$ kann jede beliebige Seite des Dreiecks sein; $h$ muss aber die jeweils zugehörige Höhe sein. Damit kann die Formel in drei verschiedenen Formen erscheinen:

$A_{\Delta ABC}=\frac{1}{2}\cdot a \cdot h_a$

Alt: (kein alt text)Link: (kein Link)

$A_{\Delta ABC}=\frac{1}{2}\cdot b \cdot h_b$

Alt: (kein alt text)Link: (kein Link)

$A_{\Delta ABC}=\frac{1}{2}\cdot c \cdot h_c$

Alt: (kein alt text)Link: (kein Link)

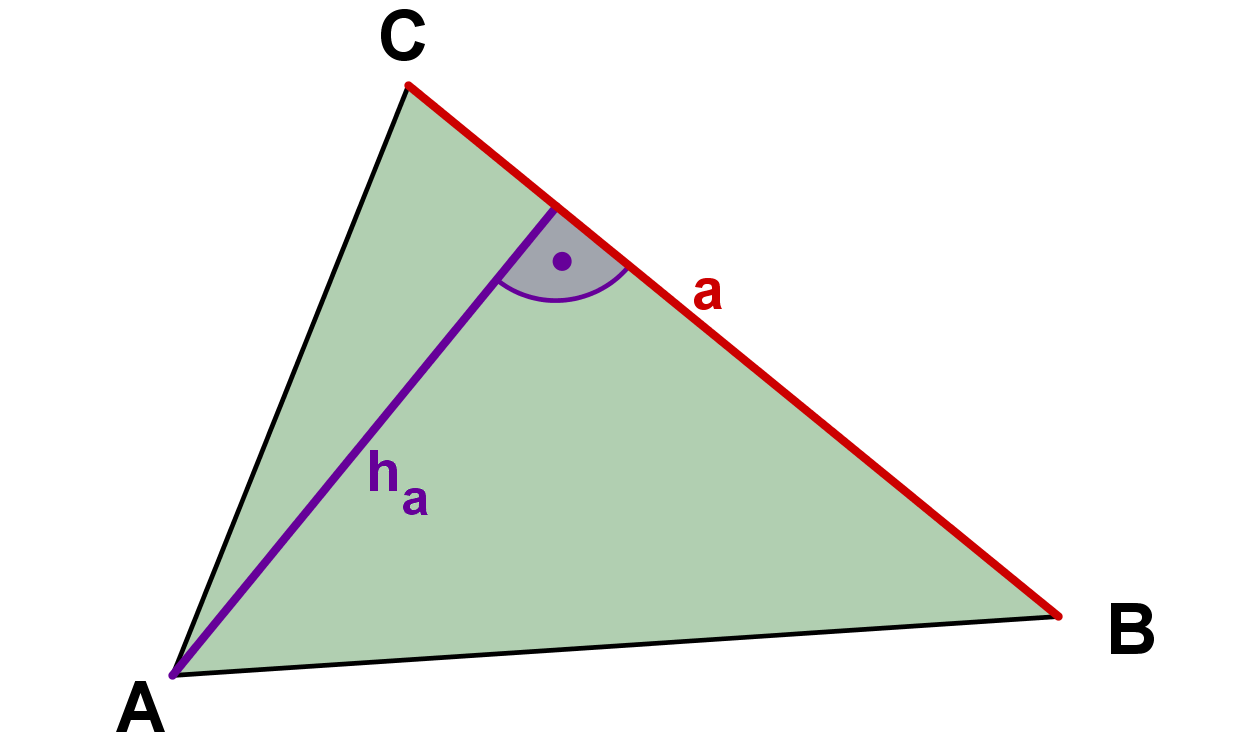
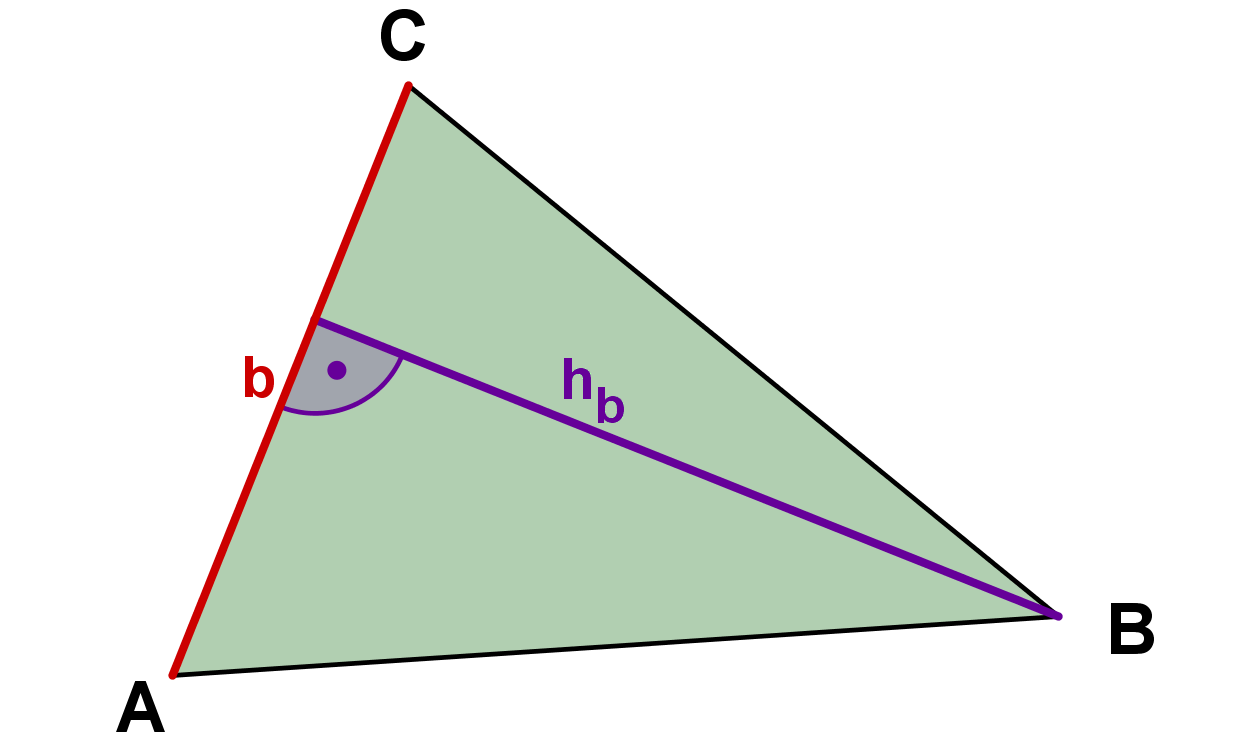
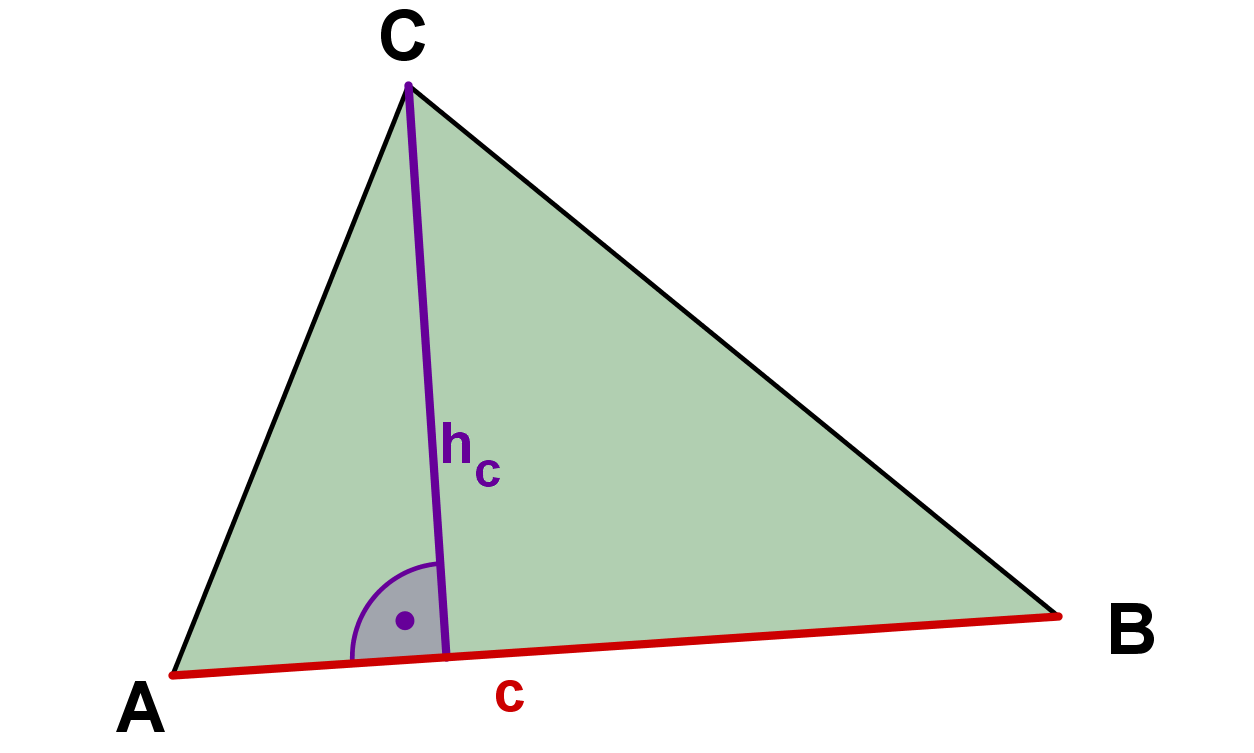
Sonderfall: rechtwinkliges Dreieck

In einem rechtwinkligen Dreieck mit den Katheten $a$ und $b$ gilt:

\displaystyle A_{\Delta ABC}=\frac{1}{2}\cdot a \cdot b

(Die Formel $A_{\Delta ABC}=\frac{1}{2}\cdot c \cdot h_c$ gilt natürlich zusätzlich immer noch.)

Grafik einfügen

Sonderfall: gleichseitiges Dreieck

In einem gleichseitigen Dreieck mit Seitenlänge $a$ gilt:

\displaystyle A_{\Delta ABC}=\frac{a^2}{4}\cdot \sqrt 3

Dreiecksfläche mit dem Sinus berechnen

Wenn man bereits den Sinus kennt und verwenden darf, kann man die Fläche eines Dreiecks auch mit Hilfe

zweier Seitenlängen und
dem Sinus des dazwischenliegenden Winkels

berechnen.

\displaystyle A_{\Delta}=\frac{1}{2}\cdot a \cdot b \cdot \sin \gamma

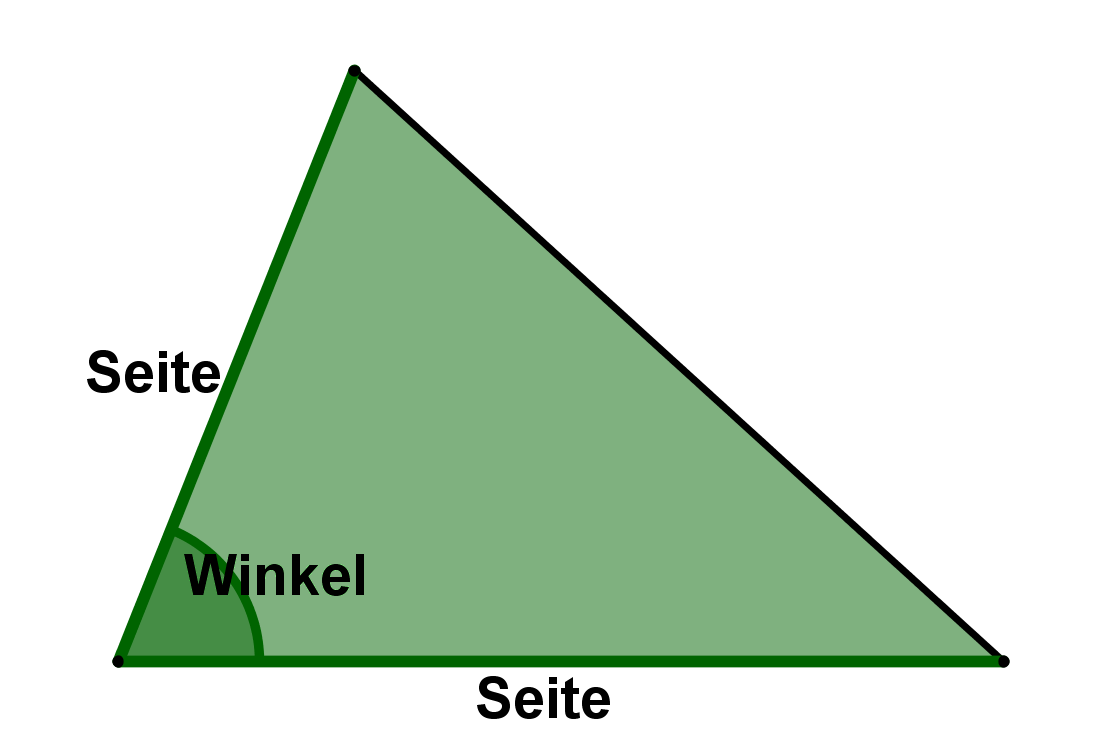
Alt: Graphik "Seite-Winkel-Seite"Link: (kein Link)

Statt $\gamma$ kann natürlich auch jeder andere Winkel des Dreiecks betrachtet werden, und daher kann die Formel auch wieder in drei verschiedenen Formen auftreten:

\displaystyle A_{\Delta}=\frac{1}{2}\cdot a \cdot b \cdot \sin \gamma

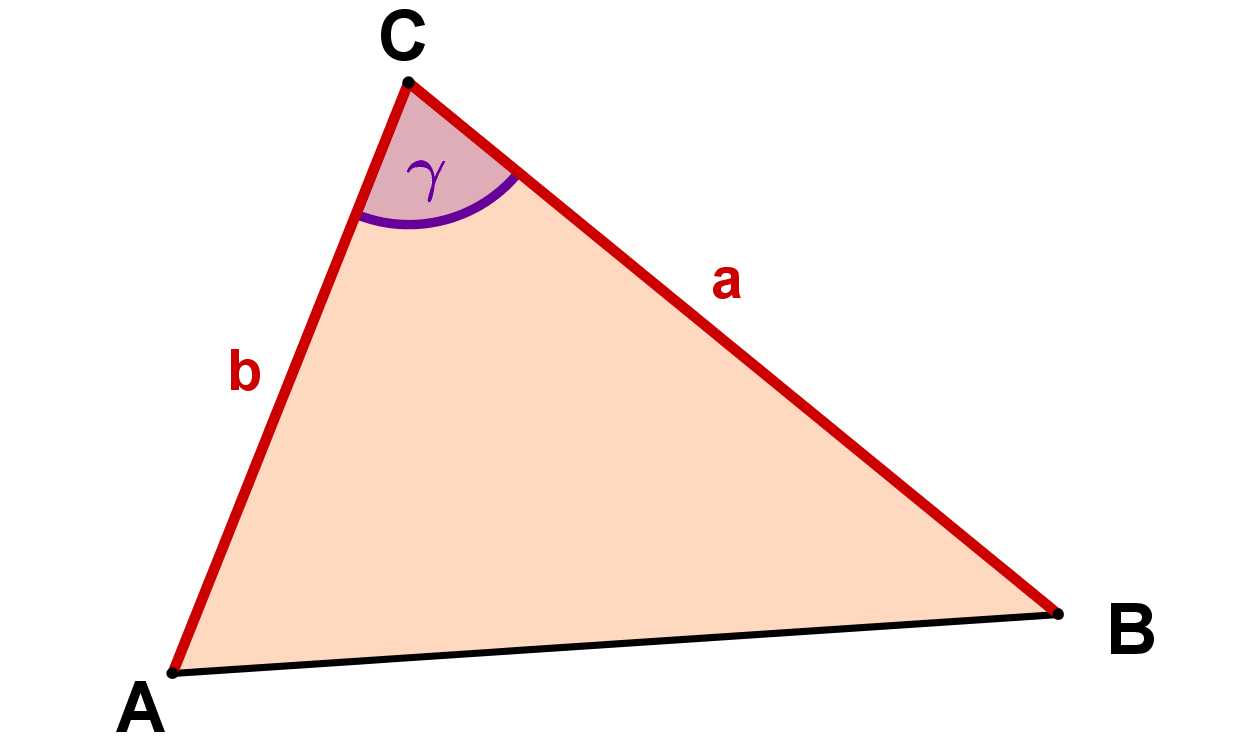
Alt: Graphik zur Veranschaulichung: Dreieck mit Seite b und Seite a und Winkel Gamma dazwischenLink: (kein Link)

\displaystyle A_{\Delta}=\frac{1}{2}\cdot a \cdot c \cdot \sin \beta

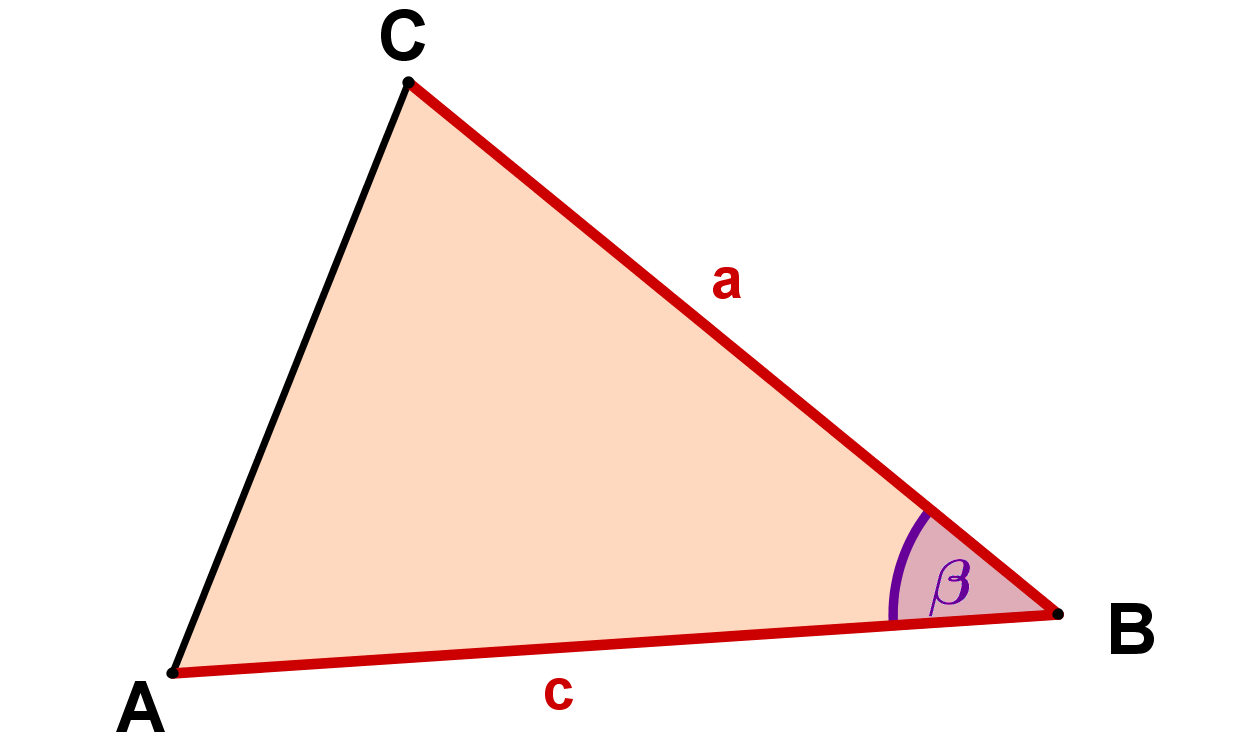
Alt: Graphik zur Veranschaulichung: Dreieck mit Seite a und Seite c und Winkel Beta dazwischenLink: (kein Link)

\displaystyle A_{\Delta}=\frac{1}{2}\cdot b \cdot c \cdot \sin \alpha

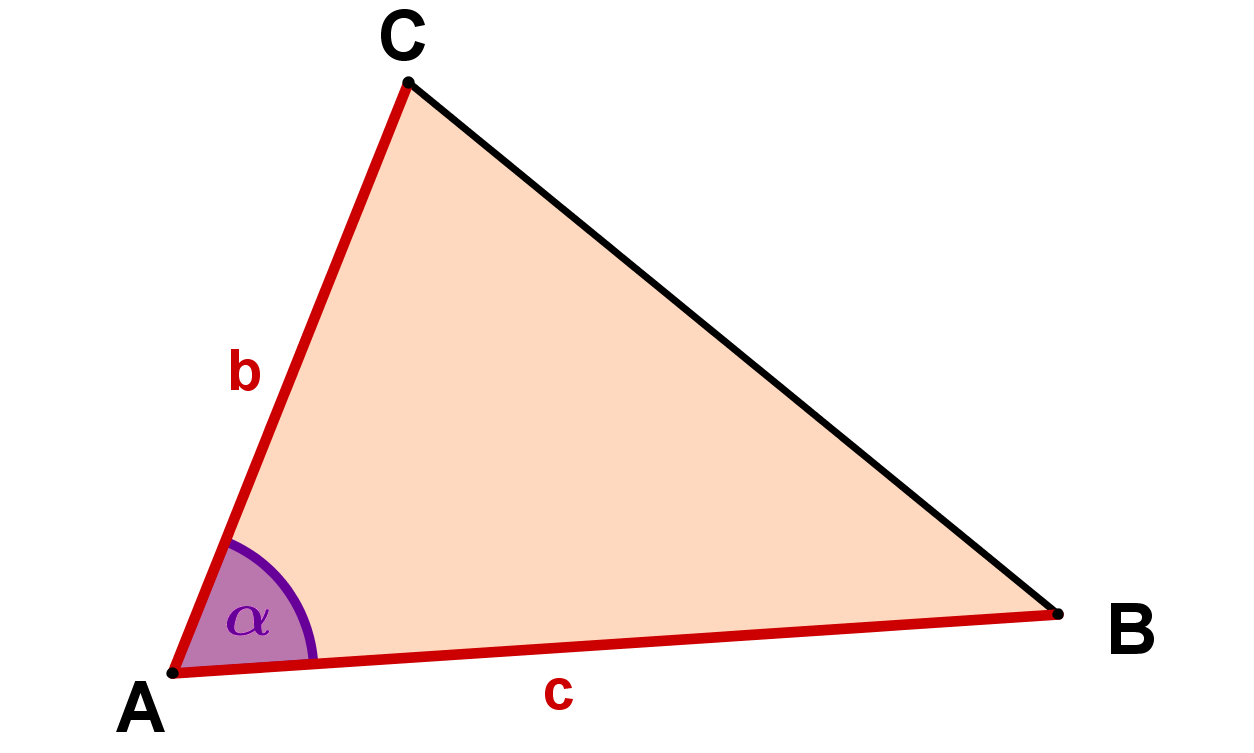
Alt: Graphik zur Veranschaulichung: Dreieck mit Seite b und Seite c und Winkel Alpha dazwischenLink: (kein Link)

Dreiecksfläche mit der Determinante berechnen

Diese Methode funktioniert natürlich nur, wenn das Dreieck in einem Koordinatensystem gegeben ist.

in Arbeit - vorerst klicke dazu hier…

Applet

url:

Meta-Beschreibung

Lerne den Flächeninhalt von Dreiecken mit verschiedenen Vorgehensweisen und Formeln zu berechnen.