Das Laplace-Gymnasium veranstaltet auf dem Sportplatz ein Fußballturnier für die neuen 5.Klassen.

An dem Turnier nehmen neun Mannschaften teil. Die Mannschaften bestehen jeweils aus Jungen und Mädchen, wobei zwei Drittel aller mitspielenden Kinder männlich sind.

a) Die drei Spielführerinnen und die sechs Spielführer der Fußballmannschaften stellen sich in einer Reihe für ein Foto auf. Bestimmen Sie die Anzahl der Möglichkeiten für die Aufstellung der neun Kinder, wenn die drei Spielführerinnennebeneinanderstehen sollen.

b) Im Rahmen der Begrüßung durch die Schulleiterin werden aus allen Spielerinnen und Spielern zunächst zehn Kinder ausgelost, die je einen Fußball erhalten sollen. Um die Wahrscheinlichkeit dafür zu berechnen, dass fünf Mädchen und fünf Jungen einen Ball erhalten, verwendet Max den Ansatz

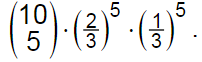
Geben Sie an, ob Max dabei vom Modell „Ziehen mit Zurücklegen“ oder vom Modell „Ziehen ohne Zurücklegen“ ausgeht. Begründen Sie rechne-risch unter Zugrundelegung eines im Sachkontext realistischen Zahlen-werts für die Gesamtzahl der Spielerinnen und Spieler, dass die von Max berechnete Wahrscheinlichkeit nur geringfügig von der tatsächlichen Wahrscheinlichkeit abweicht.

Neben dem Fußballturnier werden für die Schülerinnen und Schüler auch ein Elfmeterschießen und ein Torwandschießen angeboten.