1 Umwandeln von Volumeneinheiten
Den Würfel kennst du bereits von den Körpern und Würfelnetzen.
Aber wie du sicherlich weißt, gibt es unterschiedlich große Würfel!

Daher ist es wichtig, unterschiedliche Einheiten den entsprechenden Größen zuzuordnen.
Das folgende Beispiel soll dir dies verdeutlichen:
Die Größe eines Menschen wird in der Einheit Meter (m) angegeben.
Die Entfernung von München nach Berlin hingegen aber in Kilometern (km).
Beide Einheiten beschreiben eine Länge, die eine aber eine kleinere als die andere.
Ein kleiner Würfel wird z.B. in der Einheit 1 cm³ angegeben:
Reiht man nun 10 solcher kleinen Würfel in jede Richtung (Höhe, Länge, Tiefe)
aneinander erhält man einen Würfel der Größe 1 dm³:
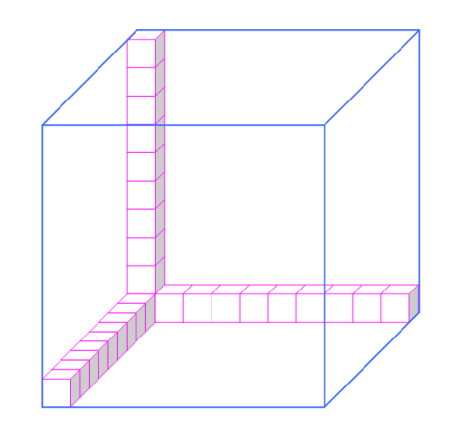
Wie viele 1 cm³ Würfel passen in den 1 dm³ Würfel? Überlege gut!
Somit ergeben sich folgende Umrechnungszahlen bei Körpern:
Einheitentabelle
Wie bei den Längen- und Flächeneinheiten auch, kann man beim Umwandeln der Volumeneinheiten die Einheitentabelle als Hilfe verwenden. Bei den Längeneinheiten ist der Umrechnungsfaktor 10. Deshalb benötigt man dort pro Einheit (m, dm oder cm) auch nur eine Spalte. Bei den Flächeneinheiten ist der Umrechnungsfaktor 100, weshalb man pro Einheit (m², cm²) zwei Spalten benötigt. Weil bei den Volumeneinheiten der Umrechnunsfaktor 1000 ist, reserviert man 3 Spalten pro Einheit (m³, cm³).

Zum Umrechnen einer Volumenangabe trägt man die angegebenene Größe bei der betreffenden Einheit ein, und zwar so, dass die Einerziffer der Zahl gerade dort steht, wo die angegebene Einheit beginnt.
Freibleibende Plätze können mit Nullen aufgefüllt werden.
Beispiel:
8375 cm³ (erste Zeile)
7002 dm³ (zweite Zeile)
8 m³ 102 cm³ (dritte Zeile)
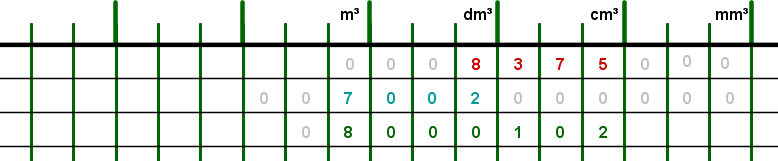
Also sind:
8375 cm³ = 8 dm³ 375 cm³
7002 dm³ = 7 m³ 2 dm³
8 m³ 102 cm³ = 8000102 cm³
Übungsaufgaben
Aufgabe 1:
Beispiel: 15 m³ = 15.000 dm³
31 m³
415 dm³
3 cm³
21 dm³
Aufgabe 2: Schreibe in der nächstgrößeren Einheit!
Beispiel: 365.000 mm³ = 365 cm³
62.000 cm³
4.650.000 dm³
400.000 mm³
5000 dm³
Aufgabe 3: Ordne der Größe nach. Beginne mit dem kleinsten.
Tipp: Wandle alle Einheiten in cm³ um!
312 dm³725.000.000 mm³47.000m³
2 Umrechnen in weitere Volumeneinheiten
Neben den schon bekannten Volumeneinheiten m³, dm³, cm³ oder mm³, bei denen die Umrechnungszahl zwischen den Einheiten immer 1000 ist, gibt es noch weitere sehr bekannte Volumeneinheiten.
So wird zum Beispiel der Inhalt einer Milchtüte nicht in m³, dm³ oder ähnlichem angegeben, sondern in Liter!
Neben den oben genannten Einheiten gibt es noch weitere Volumeneinheiten, die vorallem bei Flüssigkeiten sehr gebräuchlich sind:
Hektoliter hl
Liter l
Milliliter ml
Zentiliter cl
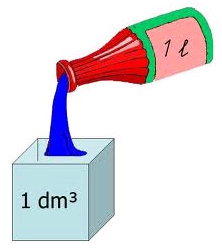
Dabei gelten folgende Umrechnungen:
1 l = 1 dm³ | 1 l = 100 cl | 1 l = 1000 ml |
|---|---|---|
1 hl = 100 l | 1 cl = 10 cm³ | 1 ml = 1 cm³ |
Übungsaufgaben:
Aufgabe 1: Wandle in Liter um!

3 hl
17 dm³
65.000 ml
38.000 cm³
500 cl
Aufgabe 2: Wandle in die angegebene EInheit um!
4 l (dm³)
3 cm³ (ml)
5 hl (l)
13 l (ml)
50 cm³ (cl)
