In diesem Kurs werden grundlegende Eigenschaften der Achsenspiegelung wiederholt und einige Konstruktionsaufgaben zum Üben zur Verfügung gestellt.

Die Achsenspiegelung kennst du schon aus der 5. Klasse. Nun wollen wir sie uns einmal genauer anschauen und einige Eigenschaften zusammentragen. Bearbeite dazu die nachfolgenden Aufträge in deinem Heft!

Aufgabe:

Im unten stehenden Bild ist das braune Dreieck durch eine Achsenspiegelung an der Achse g auf das blaue Dreieck abgebildet worden.

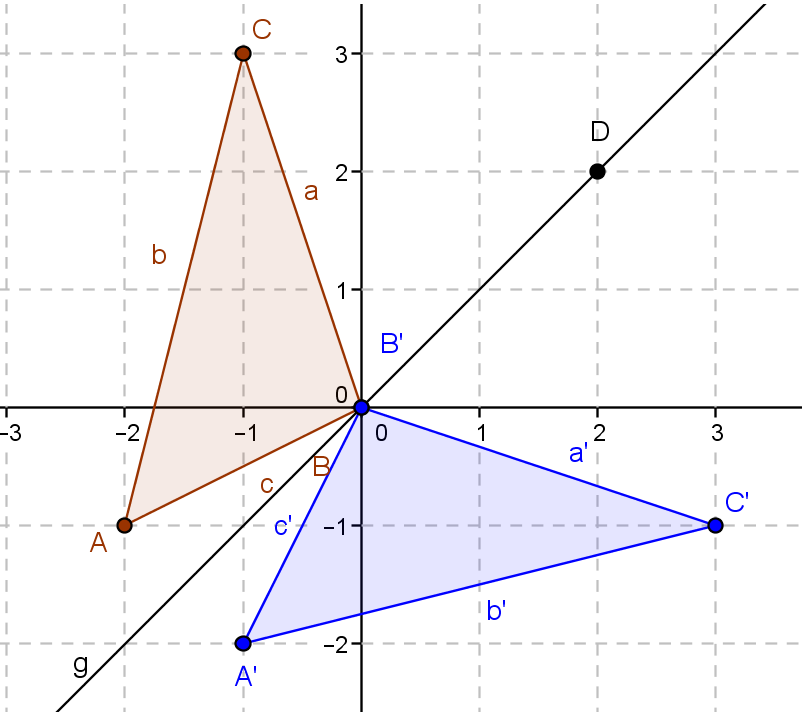
Übertrage das Bild in dein Heft im Maßstab zwei Kästchen gleich einer Längeneinheit!Alle folgenden Teilaufgaben beziehen sich auf die Zeichnung!

a) Miss nun die Länge der Seiten a, b und c, sowie a', b' und c' in deiner Zeichnung aus und notiere sie dir in einer Tabelle im Heft!

• Betrachte nun deine Messwerte. Was fällt dir dabei auf?

• Welche besondere Eigenschaft besitzt die Achsenspiegelung folglich?

b) Betrachte nun die die Innenwinkel der beiden Dreiecke! Miss dazu die Winkel $\mathrm{\angle }BAC,\mathrm{\angle }CBAund\mathrm{\angle }ACB\backslash angle\; BAC,\backslash ;\backslash angle\; CBA\backslash ;und\backslash ;\backslash angle\; ACB$, sowie die Winkel $\mathrm{\angle }{C}^{\mathrm{\prime }}{A}^{\mathrm{\prime }}{B}^{\mathrm{\prime }},\mathrm{\angle }{A}^{\mathrm{\prime }}{B}^{\mathrm{\prime }}{C}^{\mathrm{\prime }}und\mathrm{\angle }{B}^{\mathrm{\prime }}{C}^{\mathrm{\prime }}{A}^{\mathrm{\prime }}\backslash angle\; C\text{'}A\text{'}B\text{'},\backslash ;\backslash angle\; A\text{'}B\text{'}C\text{'}\backslash ;und\backslash ;\backslash angle\; B\text{'}C\text{'}A\text{'}$!

• Wie groß sind die einzelnen Winkel?

• Was fällt dir bei der Größe der Winkel auf?

• Welche besondere Eigenschaft besitzt die Achsenspiegelung folglich?

c) Betrachte nun die Lage der Punkte B und B'!

• Was fällt dir dabei auf?

• Was gilt also für alle Punkte, die bei der Achsenspiegelung auf der Symmetrieachse liegen?

• Welche besondere Eigenschaft besitzt die Achsenspiegelung folglich?

d) Aus Teilaufgabe c) bleibt festzuhalten, dass der gespiegelte Punkt B' genau dem Ausgangspunkt B entspricht. Dieser Punkt B liegt auf der Spiegelachse und wird als Fixpunkt bezeichnet.

• Was gilt also für alle Punkte, die bei einer Achsenspiegelung auf der Symmetrieachse liegen?

Da die Symmetrieachse aus lauter solchen Fixpunkten besteht, hat sie einen besonderen Namen. Sie heißt Fixpunktgerade.

e) Betrachte nun die Größen des braunen und des blauen Dreiecks!

Stell dir vor, du würdest sie ausschneiden und aufeinander legen…

• Was fällt dir auf, wenn du nun das Ausgangsdreieck und das Spiegelbild in Gedanken aufeinander gelegt hast und du es betrachtest?

• Welche besondere Eigenschaft besitzt die Achsenspiegelung folglich?

f) Betrachte nun genau die Beschriftung der beiden Dreiecke. Achte dabei besonders auf den Umlaufsinn!

• Was fällt dir dabei auf?

• Welche besondere Eigenschaft besitzt die Achsenspiegelung folglich?

Eine Achsenspiegelung ist längen-, geraden- und winkeltreu. Folglich ist diese auch kreistreu.

a) Zeichne die unten stehende Figur in dein Heft ab und vervollständige sie!

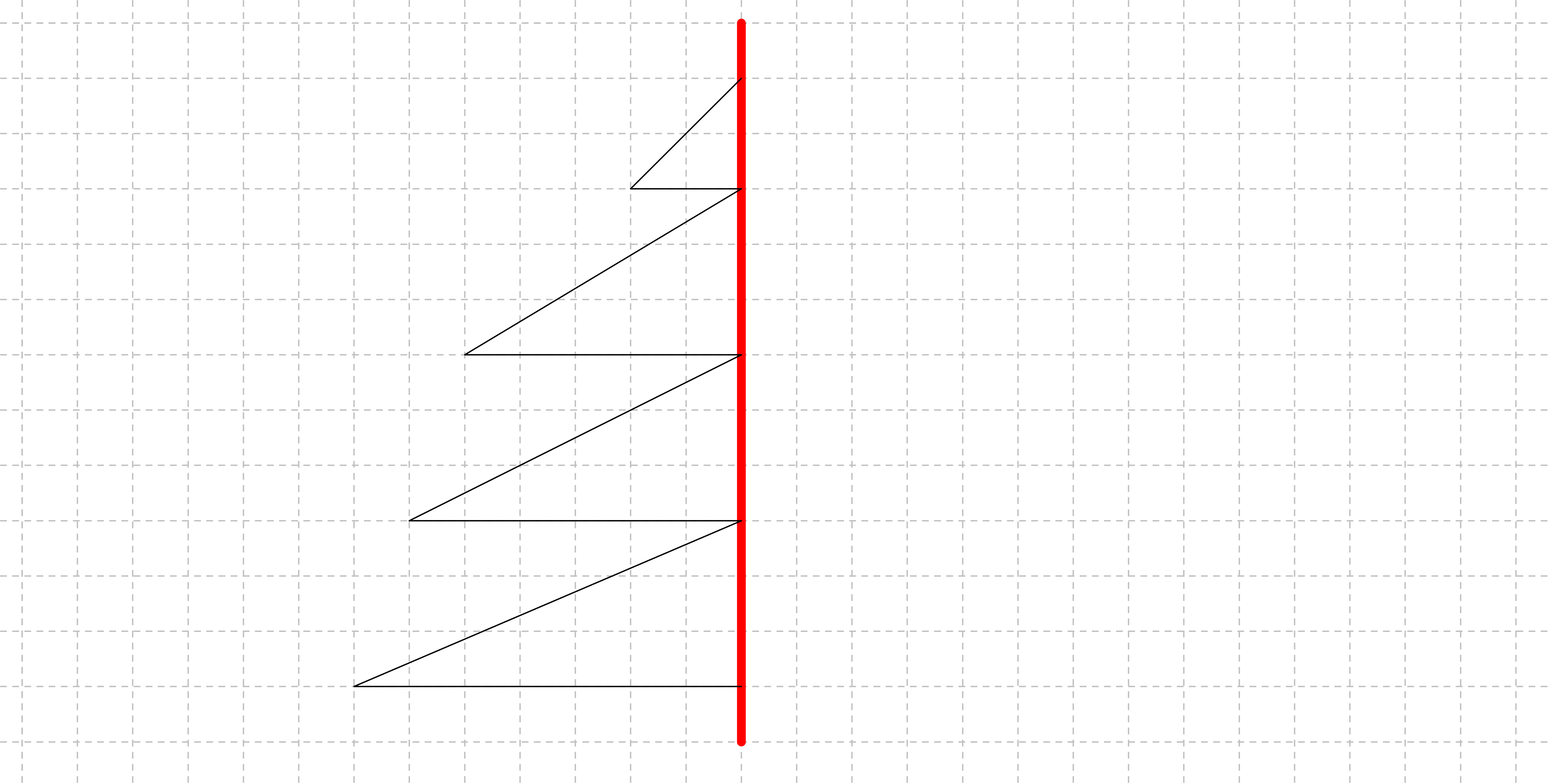
b) Verbinde nun die ursprünglichen Punkte jeweils mit ihren zugehörigenBildpunkten in deinem Heft mit einem farbigen Stift(außer rot).

c) Welche besondere Lagebeziehung besteht zwischen der rotenSymmetrieachse und den farbigen Verbindungsstrecken von Punkt undBildpunkt?

d) Überleg nun, wie du die Bildpunkte zeichnen könntest, ohne die Kästchen zuzählen. Tipp: Du könntest ein geometrisches Messinstrument zu Hilfe nehmen.

Jetzt ist es aber an der Zeit, einmal selbst ein paar Achsenspiegelungen zu zeichnen und sich mit dem Thema genauer zu beschäftigen.

Bearbeite nun den Abschnitt "Konstruktionsaufgaben". Viel Spaß!

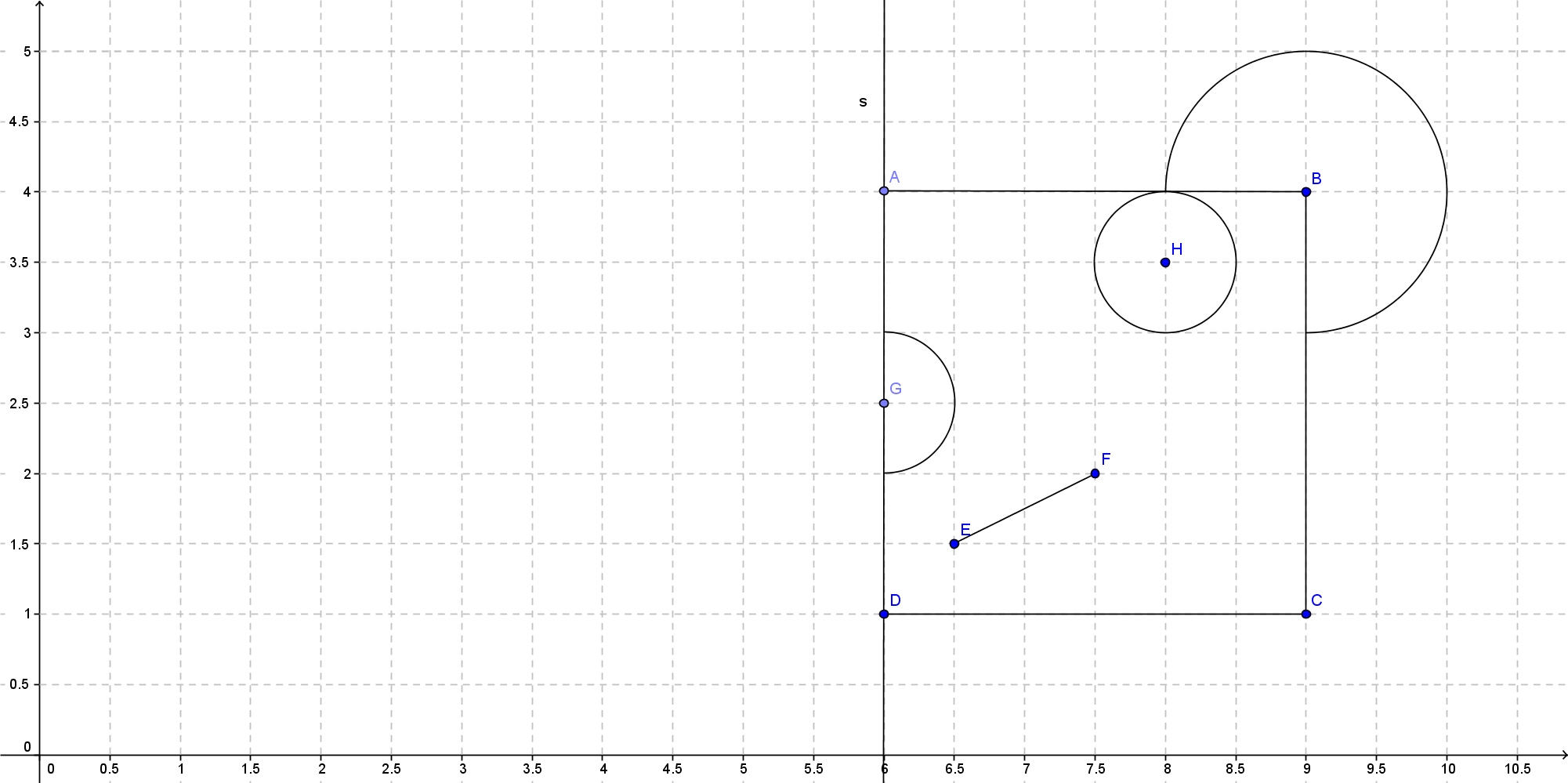
Aufgabe 1:

Spiegele die Urpunkte an der Spiegelachse s und ergänze die Figur!

Aufgabe 2:

A(6|5); B(9|5); C(9|1); D(6|1); E(6,5|1,5); F(7|2); G(6|3); H(8|4).Zeichne die Spiegelachse s durch die Punkte A, G und D und spiegele die oben genannten Punkte an dieser Achse.

a)

b)