1 Überblick
Dieser Kurs führt grundlegende Begriffe aus der Geometrie ein und greift auch Themen aus dem Kurs "Achsenspiegelung" auf.
2 Abstand und Winkel
Aufgaben:
1.
Laden
2.
Laden
3.
Laden
3 Symmetrieachsen und Grundkonstruktionen
Aufgabe:
a) Zeichne die Punkte und in ein Koordinatensystem ein und spiegele diese Punkte an der Gerade, die durch den Koordinatenursprung und den Punkt verläuft!
b) Finde jeweils alle Symmetrieachsen in den folgenden Figuren!
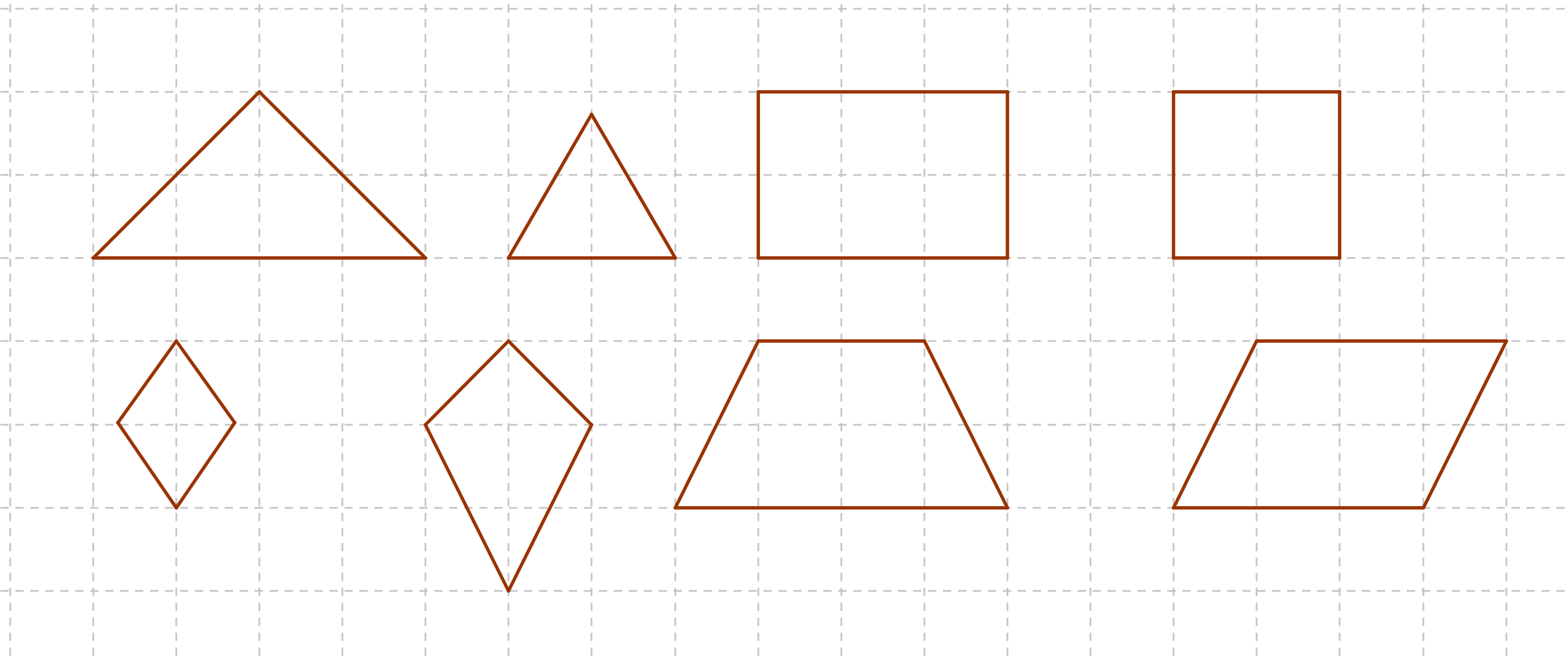
c) Wiederhole die Grundkonstruktionen zu Mittelsenkrechte, Winkelhalbierende und Fällen eines Lotes. Zeichne jeweils folgende Objekte in ein Koordinatensystem:
1.Die Punkte und . Konstruiere die Mittelsenkrechte der Strecke [].
2.Die Punkte und . Konstruiere die Winkelhalbierende des Winkels .
3.Die Gerade g durch die beiden Punkte und . Fälle das Lot von auf die Gerade g.
4 Gerade, Halbgerade und Strecke
1.Lege eine Halbgerade von durch und zeichne um einen Kreis mit Radius 2 cm.
a) Zeichne eine zu g parallele Gerade h durch A und benenne beide Geraden mit mathematischen Fachausdrücken.
b) Bestimme den Abstand des Punktes von der Geraden .
c) Zeichne den Durchmesser des Kreises ein, der senkrecht zur Geraden verläuft.
d) Zeichne eine Tangente ein.
2.Benenne die Objekte a) bis f) mit mathematischen Fachausdrücken.
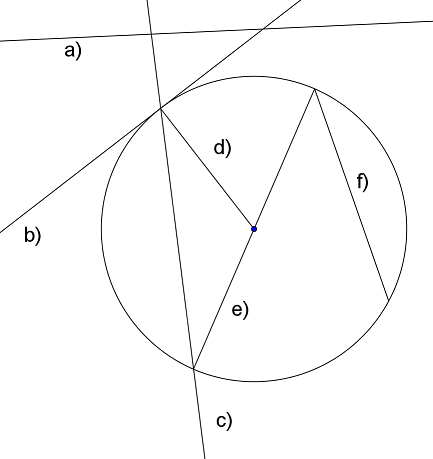
3.Gegeben sind und .
a) Zeichne .
b) Zeichne so, dass gilt: und .
c) Zeichne so, dass gilt: und .
d) Zeichne das Lot von auf .
e) Miss .
5 Winkel im Koordinatensystem
1.
Laden
2.
Laden
3.
Laden
4.
Laden
