1 Grundlagen zur Menge der ganzen Zahlen
a) Negative Zahlen sind dir bereits aus dem Alltag bekannt, etwa aus folgenden Situationen:
Temperatur, z.B. Celsius
Anzeige im Aufzug, z.B. Etage -1 (1. Untergeschoss)
Höhen von Orten, z.B. totes Meer -5m ü.NN. (Normalnull)
b) Die Vereinigung der negativen Zahlen mit den nichtnegativen Zahlen ergibt die Menge der ganzen Zahlen :
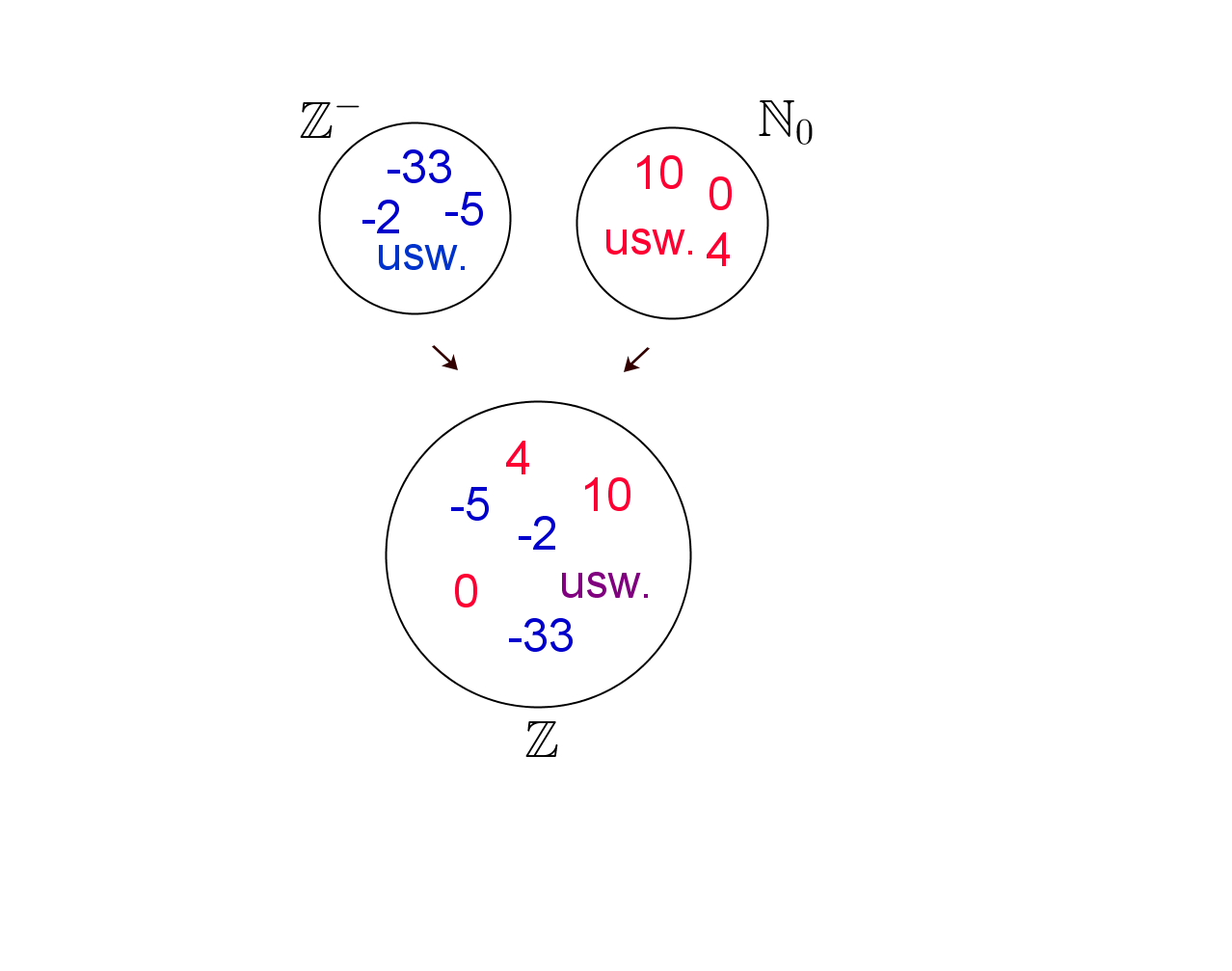
c) Die Menge der ganzen Zahlen lässt sich auch gut am Zahlenstrahl veranschaulichen. Dabei stehen die negativen Zahlen links von der und die positiven rechts davon.
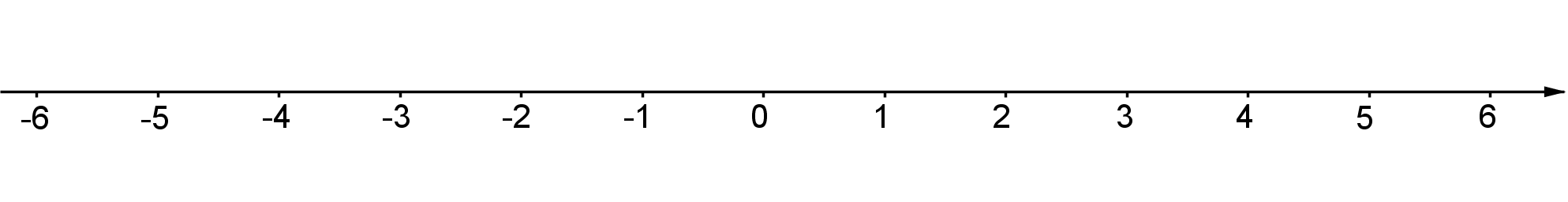
Der Abstand einer ganzen Zahl von der 0 wird als ihr Betrag bezeichnet. Damit ist der Betrag einer positiven Zahl die Zahl selbst. Beispiel: Der Betrag von ist , in Zeichen: .
Zu einer Zahl heißt die Zahl auf der anderen Seite der mit gleichem Betrag Gegenzahl.Beispiel: Die Gegenzahl zu ist .
d) Nun wollen wir uns mit der Addition ganzer Zahlen beschäftigen. Dabei wollen wir die Addition einer positiven Zahl durch einen nach rechts zeigenden Pfeil veranschaulichen. Wird eine negative Zahl addiert, so nutzen wir einen nach links zeigenden Pfeil.
Beispiel:
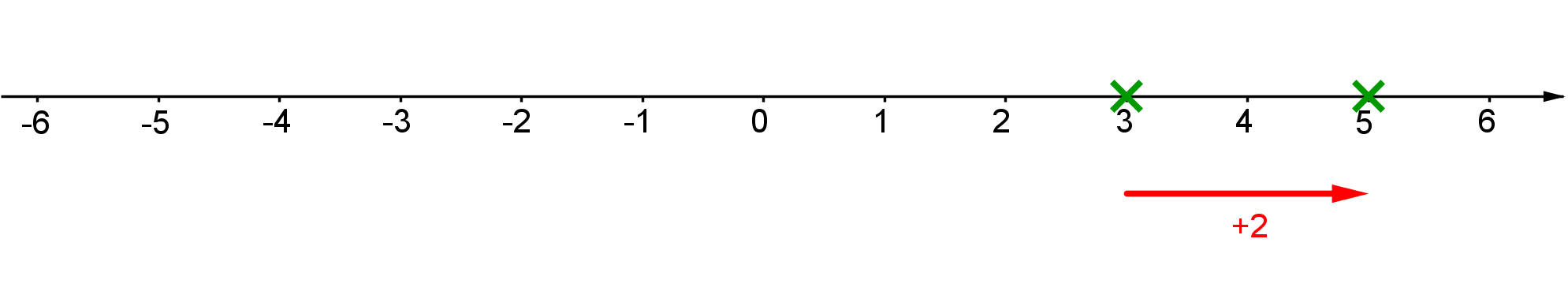
Beispiel:

e) Bei der Subtraktion ganzer Zahlen sehen wir den Bezug zur Addition. Hier stellen wir die Subtraktion einer negativen Zahl, die der Addition der Gegenzahl entspricht, mit einem nach rechts zeigenden Pfeil dar.
Beispiel:
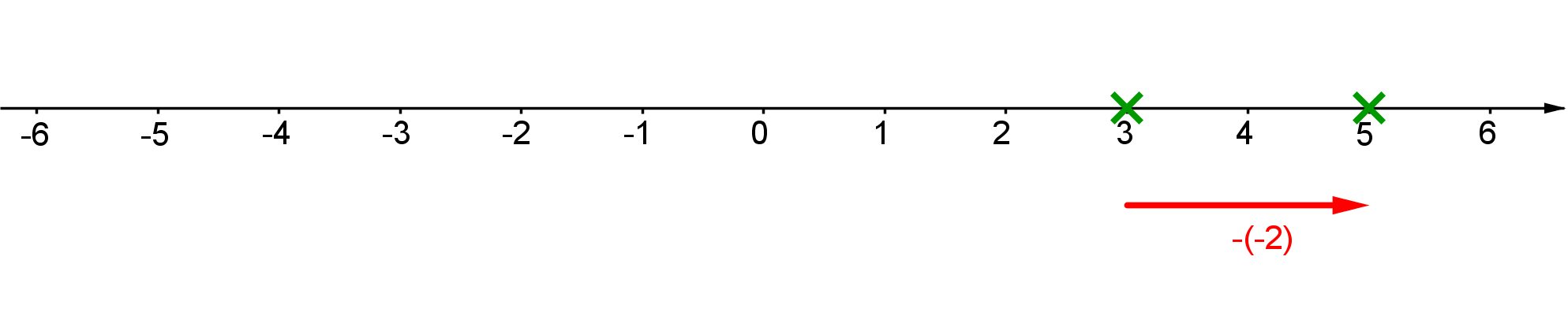
Beispiel:

2 Übungsaufgaben - einfach
1.
2.
3.
Laden
3 Übungsaufgaben - mittel
1.
Laden
2.
Laden
3.
Laden
