Drei und mehr Klammern ausmultiplizieren

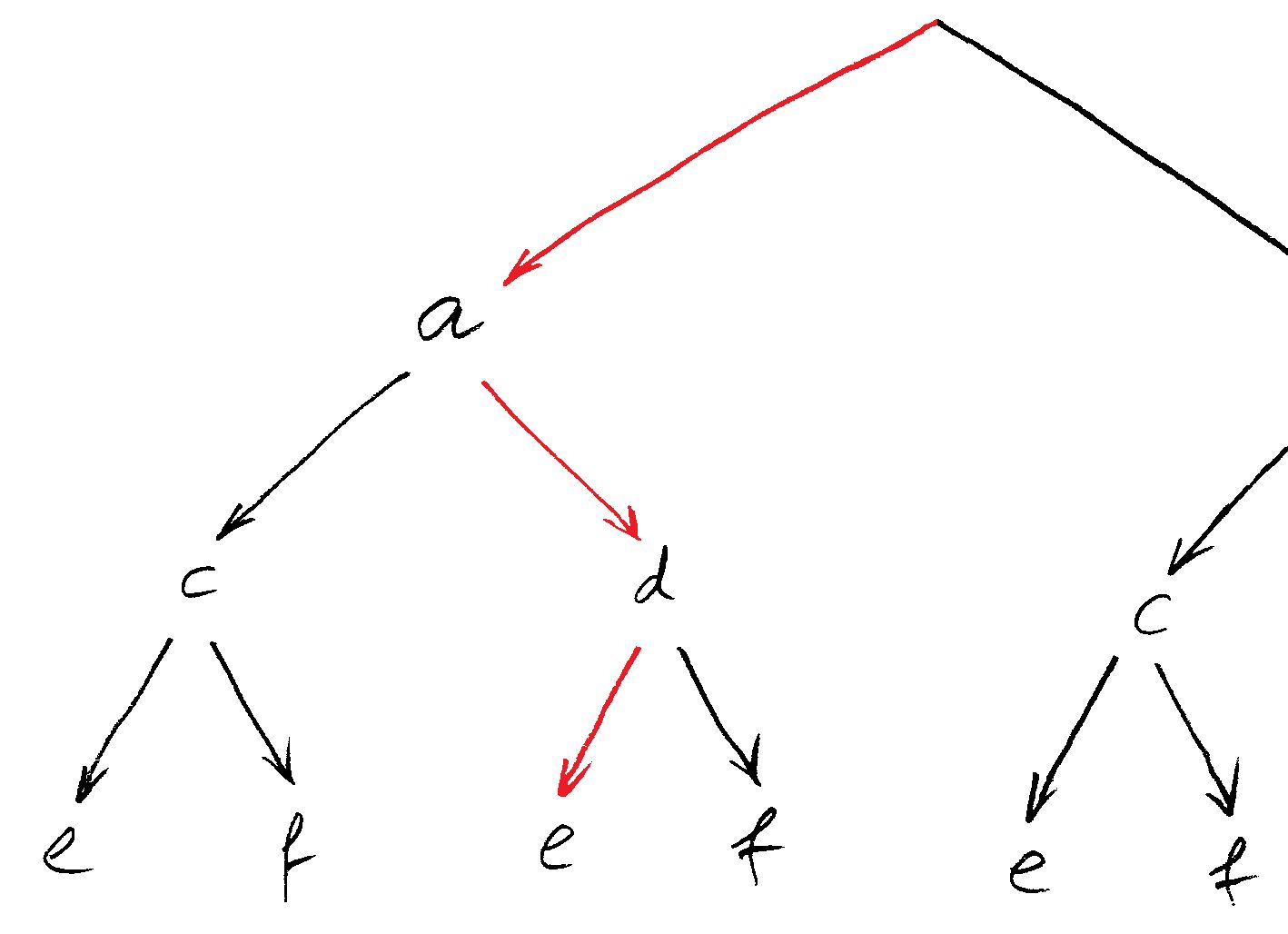
Baum-Schema

Du willst das Produkt der drei Klammern

$(a+b)\cdot(c+d)\cdot(e+f)$

ausmultiplizieren.

Dazu zeichnest du einen Baum mit drei Ebenen. Die erste Ebene beschriftest du mit den Summanden der ersten Klammer, die zweite Ebene mit den Summanden der zweiten Klammer und die dritte Ebene mit den Summanden der dritten Klammer. Achte darauf, dass du den Baum breit genug zeichnest:

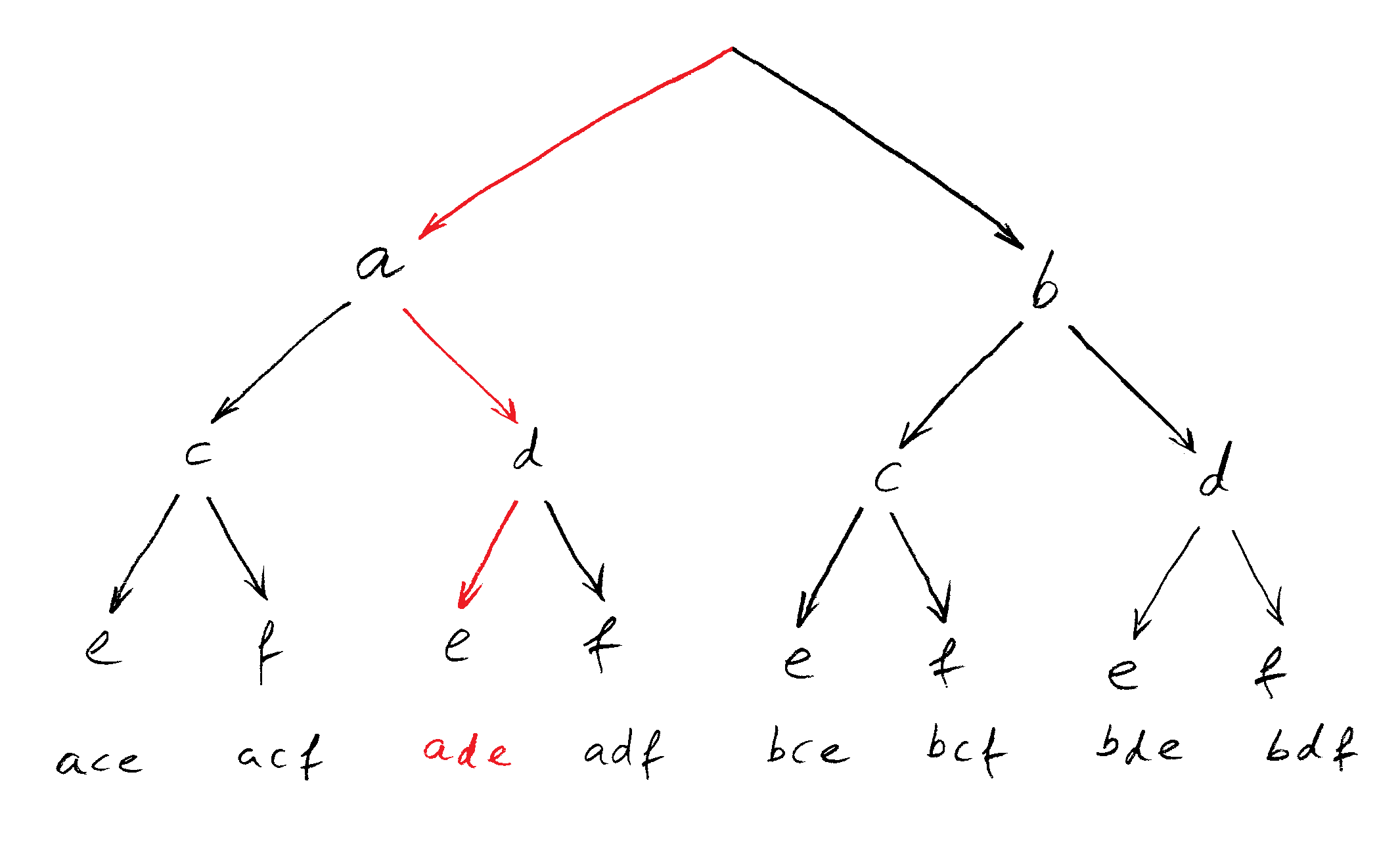
Und nun liest du entlang der Pfeile von oben nach unten die Produkte ab, die du beim Ausmultiplizieren erhältst und schreibst sie unter den Baum; der Weg beispielsweise zum Produkt $ade$ ist hier rot gekennzeichnet. Von diesen Produkten bildest du die Summe:

$ace + acf + ade + adf + bce + bcf + bde + bdf$

Dies ist das Ergebnis des Ausmultiplizierens der drei Klammern!

Vorteile

Vielleicht findest du es zu umständlich, extra ein solches Baum-Schema zu zeichnen. Aber so kannst du sehr leicht noch einmal nachkontrollieren,

• ob du alle Produkte erfasst hast,

• ob du diese Produkte richtig gebildet hast,

• ob alle Vorzeichen stimmen.

Der letzte Punkt ist bei dem angegebenen Beispiel noch ohne Bedeutung, jedoch dann, wenn Minuszeichen in den Klammern vorkommen, so etwa in folgendem Beispiel.

Klammern mit Minuszeichen

Du willst das Produkt der drei Klammern

$(a+b)\cdot(c-d)\cdot(e-f)$

ausmultiplizieren.

Dazu zeichnest du wieder das entsprechende Baum-Schema und achtest dabei auf die Minuszeichen (vor dem $d$ und vor dem $f$):

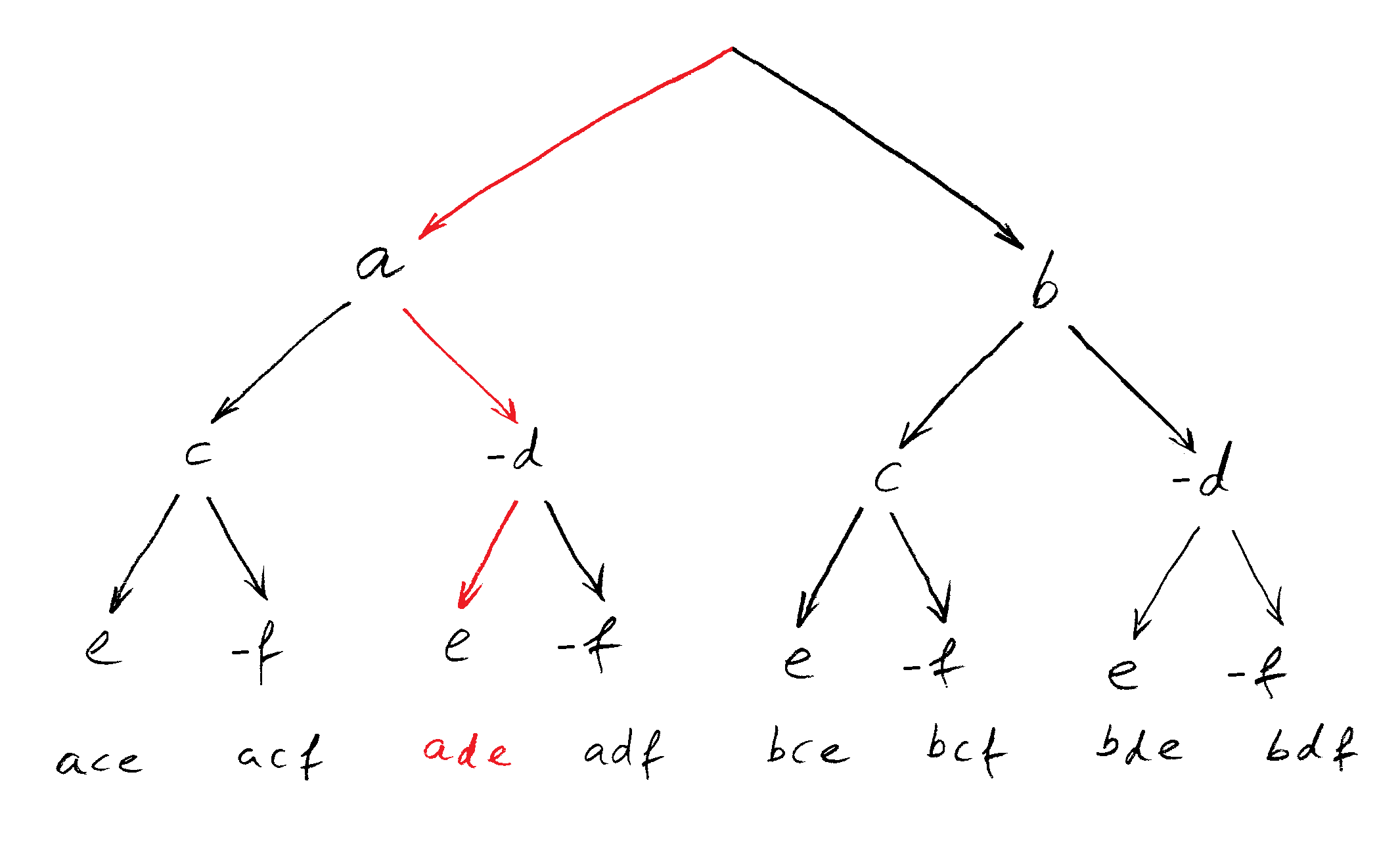
Danach liest du wieder entlang der Pfeile die zugehörigen Produkte ab und schreibst sie unter den Baum. Ein Tipp: Berücksichtige erst einmal die Vorzeichen nicht!

Erst wenn du die Summe der Produkte bildest, dann fügst du jeweils vor ein Produkt

• ein Minuszeichen ein, wenn auf dem Weg zu diesem Produkt eine ungerade Anzahl von Minuszeichen vorkommen (also 1 oder 3 Minuszeichen)

• ein Pluszeichen ein, wenn auf dem Weg zu diesem Produkt eine gerade Anzahl von Minuszeichen vorkommen (also 0 oder 2)

Damit erhältst du das Ergebnis

$ace - acf - ade + adf + bce - bcf - bde + bdf$

Denn auf dem Weg zum Produkt $ade$ kommt 1 Minuszeichen vor, deshalb schreibst du vor $ade$ ein Minuszeichen. Auf dem Weg zu $adf$ kommen dagegen 2 Minuszeichen vor, deshalb schreibst du vor $adf$ ein Pluszeichen (denn Minus mal Minus gibt Plus).

Noch ein Beispiel

Du willst das Produkt der drei Klammern

$(a^2-x)\cdot(2a+5)\cdot(x-3)$

ausmultiplizieren.

Du zeichnest wieder das entsprechende Baum-Schema, dabei achtest du auf die Minuszeichen (vor dem $x$ und vor der 3):

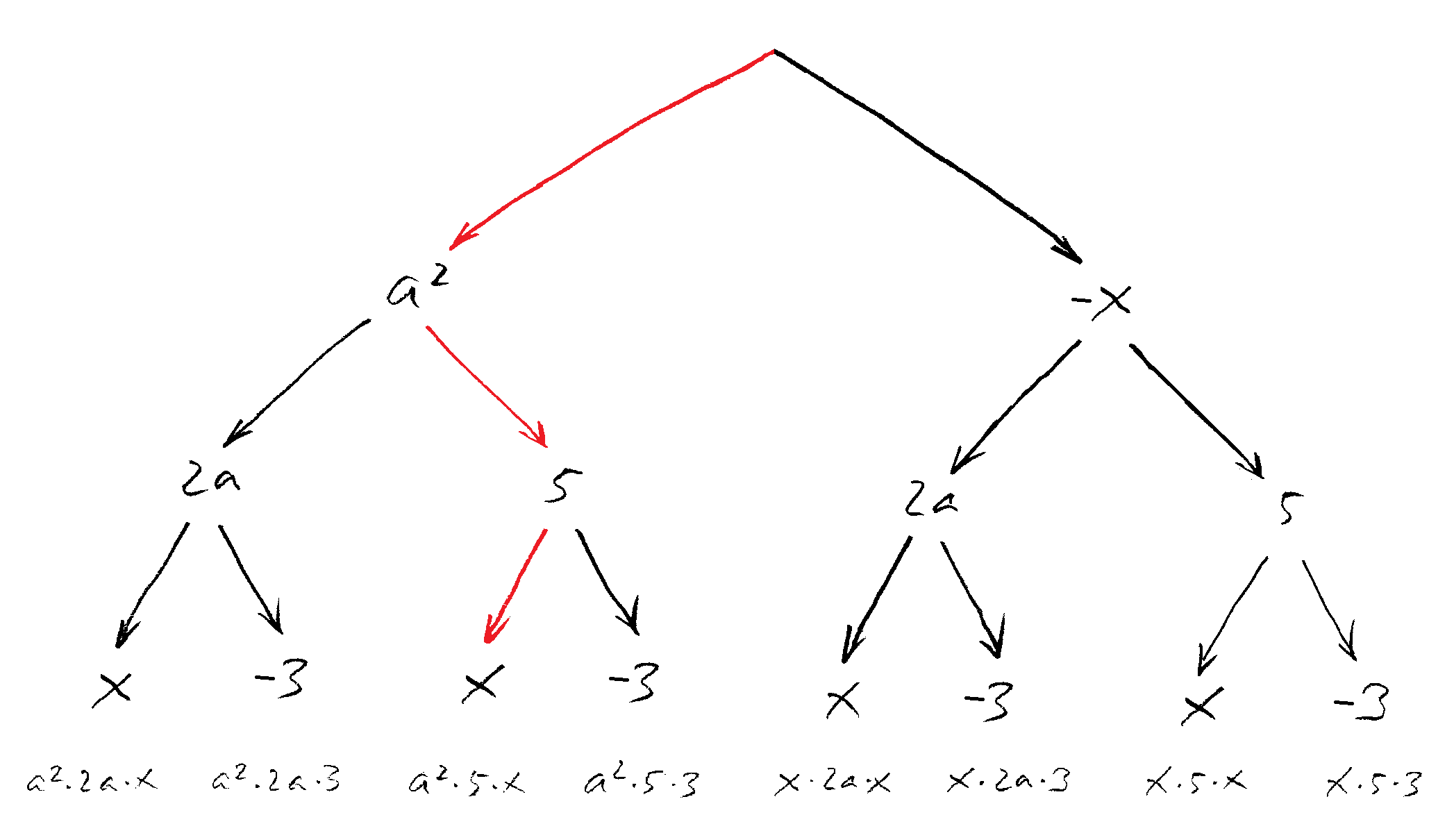
Du liest wieder entlang der Pfeile die zugehörigen Produkte ab und schreibst sie unter den Baum. Die Vorzeichen berücksichtigst du erst einmal nicht!

Wenn du aber dann die Summe der Produkte bildest, fügst du jeweils vor ein Produkt ein Minus- oder ein Pluszeichen ein, je nachdem, ob du auf dem Weg zu diesem Produkt einer ungeraden oder einer geraden Anzahl von Minuszeichen begegnest.

Damit erhältst du das Ergebnis

$a^2\cdot 2a\cdot x - a^2\cdot 2a\cdot 3 + a^2\cdot 5\cdot x - a^2\cdot 5\cdot 3 - x\cdot 2a\cdot x + x\cdot 2a\cdot 3 - x\cdot 5\cdot x + x\cdot 5\cdot 3$

Diesen Ausdruck vereinfachst du noch zu

$2a^3x - 6a^3 + 5a^2x - 15a^2 -2ax^2 + 6ax - 5x^2 + 15x$

Fazit

Solche komplizierten Ausdrücke wie im vorigen Beispiel sind der blanke Horror, besonders wenn du in der Mathe-Arbeit unter Stress stehst. Selbst du als Mathe-Genie vertust dich dann schnell mal bei einem Vorzeichen. Um sicherzugehen, dass dies nicht passiert, rechnest du die ganze Aufgabe noch einmal von vorn - und machst womöglich noch einmal denselben Fehler.

Deshalb ist es so wertvoll, dass du ein solches Schema wie hier zur Verfügung hast. Dann kannst du sehr kleinteilig jeden Rechenschritt noch einmal einzeln überprüfen, sodass du dir am Ende sicher bist, dass deine Lösung richtig ist.

Du kannst auch noch kompliziertere Klammern wie $(a+b)\cdot(a^2 + 2ab + b^2)\cdot(a+b)$ ausmultiplizieren. Dann verzweigt sich der Baum in seinen Ebenen entsprechend oft, hier also in der zweiten Ebene dreifach.

Probiere es selbst einmal aus! Überzeuge dich selbst von den Vorteilen dieser Methode! Rechne zum Beispiel die binomische Formel $(a+b)^3$ aus. Oder bearbeite noch andere der folgenden Übungsaufgaben.

Theoretisch kannst du mit dem Baum-Schema nicht nur 3, sondern auch 4 oder 5 oder 6 Klammern ausmultiplizieren. Aber der Baum wird dann sehr groß (vor allem sehr breit).

Und du kannst mit dem Baum-Schema natürlich auch 2 Klammern ausmultiplizieren. Probiere einmal aus, ob dir bei 2 Klammern das Baum-Schema oder die Tabellen-Methode besser gefällt.