Eine Architektin plant den Bau eines einstöckigen Hauses. Dazu stellt sie das Haus modellhaft in einem kartesischen Koordinatensystem des dar. Im Modell wird das Haus aus einem Quader und einem dreiseitigen, geraden Prisma zusammengesetzt. Gegeben sind die Punkte , , und . Die Koordinaten der Punkte sind Längenangaben in der Einheit Meter. Die Deckenhöhe im Erdgeschoss beträgt .
Bei den Rechnungen kann auf das Mitführen der Einheiten verzichtet werden. Runden Sie Ihre Ergebnisse sinnvoll.
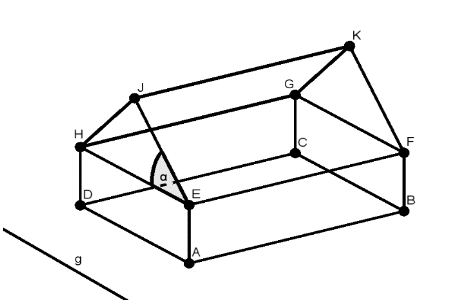
Zeigen Sie, dass der Punkt die Koordinaten besitzt. Überprüfen Sie rechnerisch, ob die Grundfläche des geplanten Hauses im Punkt rechtwinklig ist.
Eine Grundstücksgrenze des Baugrundstückes verläuft entlang der Geraden
g: mit .
Die Punkte und liegen auf der Geraden . Untersuchen Sie die gegenseitige Lage der Geraden und .
Ermitteln Sie die Maßzahl des Gesamtvolumens des Hauses.
Für den Dachneigungswinkel (siehe Aufgabe Aufgabenstellung) gilt gemäß der örtlichen Bauvorschrift . Zeigen Sie, dass der Dachneigungswinkel die Bauvorschrift erfüllt.
Im Dachgeschoss soll eine Zwischendecke eingezogen werden, die parallel zur Grundfläche und einen Meter tiefer als der First ist. Diese Zwischendecke liegt in der Ebene . Bestimmen Sie eine Gleichung der Schnittgeraden der Ebene mit der durch gegebenen Ebene.
Zur Bewässerung des Gartens soll Regenwasser, das auf das Hausdach trifft, in einer Zisterne gesammelt werden. Gemäß statistischer Daten der letzten Jahrzehnte ist die durchschnittliche gesamte Niederschlagsmenge im sonnenreichen Juli . Zur Bewässerung des großen Gartens sind zusätzlich täglich notwendig. Entscheiden Sie mithilfe einer Rechnung, ob die Bewässerung im Monat Juli gemäß der statistischen Daten durchgeführt werden kann. Vereinfachend wird von störenden Einflüssen wie etwa Wind abgesehen und angenommen, dass der Regen parallel zur -Achse fällt.
