1 Übersicht
Inhalt des Kurses
Dieser Kurs gibt eine Einführung zum Runden natürlicher Zahlen sowie der Größen wie Geld, Länge, Masse und Zeit.
Benötigte Vorkenntnisse
Für diesen Kurs solltest du folgenden Vorkenntnisse haben:
Du solltest große Zahlen bis zu oder höher kennen.
Du solltest wissen, was Zehner-, Hunderter-, Tausenderzahlen usw. sind.
Du solltest den Zahlenstrahl kennen.
Außerdem:
Du solltest wissen, in welchen Einheiten man Geldbeträge, Längen, Massen und Zeit angibt.
2 Was ist "Runden"? (Beispiel 1)
Stolz sagt der Theaterbesitzer zum Zeitungsreporter:
„Heute haben wir 1003 Eintrittskarten verkauft!“
Am nächsten Tag steht in der Zeitung:
„Für die Vorstellung gestern abend wurden rund 1000 Karten verkauft.“

Zum Nachdenken:
3 Was ist "Runden"? (Beispiel 2)
Frau Müller zum Verkäufer:
"Entschuldigung, ich brauche 30 schöne Erdbeeren zum Dekorieren der Tortenstücke für Opas Geburtstag. Wie viele einzelne Erdbeeren sind in diesen vier 500g-Schalen zusammen?"
Verkäufer:
"Oh, ich denke, so ungefähr 40 Stück."
Als Frau Müller die Erdbeeren später zu Hause zählt, stellt sie fest, dass es 38 Erdbeeren sind.

Zum Nachdenken
4 Was ist "Runden"?
Beim Runden einer Zahlenangabe gibt man einen Wert an, der nicht genauso groß zu sein braucht wie der wirkliche Wert, sondern nur ungefähr so groß.
Man schreibt daher statt des normalen "Ist-Gleich"-Zeichens ein gewelltes "Ist-ungefähr-gleich"-Zeichen, das so aussieht:
1003 Karten 1000 Karten,
→ denn 1003 Karten sind nicht dasselbe wie 1000 Karten, aber ungefähr dasselbe.
5 Was ist "Runden"?
Dieser ungefähre Wert sollte dafür aber "rund" sein.
Zum Nachdenken:
"1003 Karten" ist keine runde Zahl, sondern eine genaue Angabe.
→" 1000 Karten" ist ein "runder" Wert, denn 1000 ist eine Zehner-, Hunderter- und sogar eine Tausenderzahl.
"38 Erdbeeren" ist eine genaue Angabe.
→" 40 Erdbeeren" ist als Mengenangabe "runder" als "38 Erdbeeren", weil 40 eine Zehnerzahl ist und 38 nicht.
6 Was sind überhaupt "runde Zahlen"?
Ob eine Zahl "rund" ist oder nicht, hängt von der Aufgabenstellung ab:
Wenn auf Zehner gerundet werden soll, sind Zehnerzahlen "rund" und es ist diejenige Zehnerzahl gesucht, die am nächsten an der Zahl liegt.
Wenn auf Hunderter gerundet werden soll, sind erst Hunderterzahlen "rund", und es ist eine Hunderterzahl gesucht.
Wenn auf Tausender gerundet werden soll, sind Tausenderzahlen "rund".
usw.
7 Warum rundet man? (3/4)
Klaus: " Von hier bis zur nächsten U-Bahn-Station sind es ungefähr ."
Sophie:"Woher willst du denn das so genau wissen?"
Klaus: "Ich habe den Kioskbesitzer gefragt; er hat gesagt, es sind ungefähr . Und der Kiosk ist von uns jetzt ungefähr entfernt."
Sophie:"Dann solltest du aber trotzdem lieber sagen, dass die U-Bahn-Station ungefähr weit weg ist."
Zum Nachdenken
Warum meint Sophie, dass Klaus lieber von "ungefähr " sprechen soll?
8 Warum rundet man? (4/4) - Ergebnis
Warum rundet man also?
Du hast nun drei Gründe kennengelernt, warum man Zahlen oder Größen rundet:
Weil man sich die gerundeten Zahlen besser vorstellen und besser merken kann.
Weil man die genauen Zahlen nicht kennt und deshalb nur ungefähre Angaben machen kann.
Weil die angegebenen Zahlen auf andern Angaben und Voraussetzungen beruhen, die selbst ungenau sind.
9 Übungsaufgaben
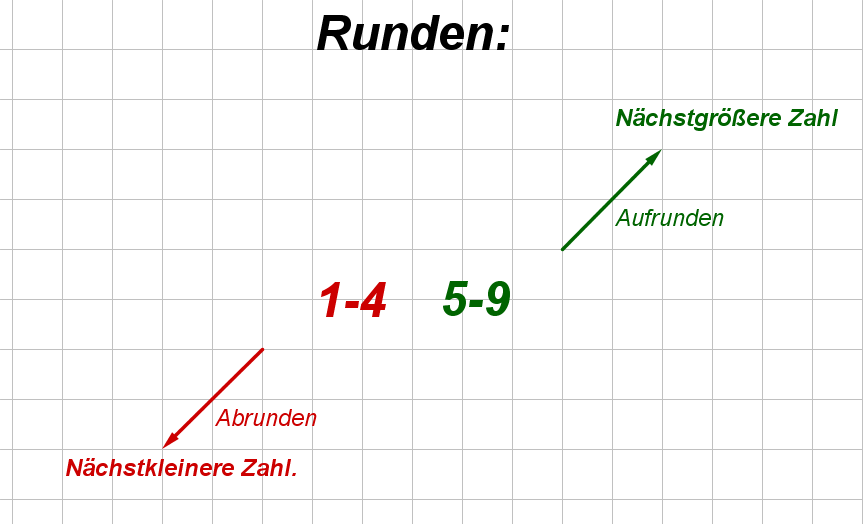
10 Wie rundet man?
Zwischen welchen beiden runden Zahlen liegt die Zahl?
11 Wie rundet man?
12 Wie rundet man?
In dem folgenden Applet wird veranschaulicht, wie man auf Zehntel rundet.