Mit Relationen kannst du Beziehungen zwischen Dingen ausdrücken. Beispielsweise kannst du mit einer Relation zwischen den Mengen und ausdrücken, welche Elemente der einen Menge mit welchen Elementen der anderen Menge in Beziehung stehen, also hier, welches Tier welchen Laut geben kann.
Veranschaulichung einer Relation
Seien Mengen. Eine Relation ist eine Teilmenge des kartesischen Produkts
Das kartesische Produkt ist die Menge der geordneten Paare mit und .
Eine Relation ist einfach irgendeine Teilmenge eines kartesischen Produkts von zwei Mengen - es kommt zunächst nicht darauf an, ob die Relation irgendeinen Sinn ergibt.
Statt schreibst du meist - insbesondere, wenn der Name der Relation kein Buchstabe wie ist, sondern irgendein schönes Symbol, z. B. oder .
Beispielsweise definierst du die Relation aus der obigen Einleitung als "kann sagen", bezeichnet mit dem Symbol , in folgender Weise:

Damit gilt beispielsweise Folgendes: Kuh "Muh", Kuh " " und Ziege "Mäh". Die Kuh kann "Muh" sagen, sie kann auch " " sagen, die Ziege kann "Mäh" sagen.
Relationen auf einer Menge
Es ist ohne Weiteres möglich, dass und dieselbe Menge sind. Man spricht dann von einer Relation auf der Menge .
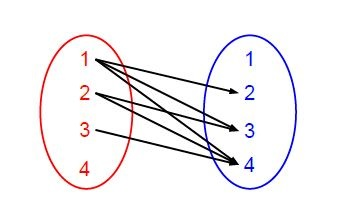
Eine Relation auf der Menge ist beispielsweise die Relation ("ist kleiner"):
Die Relation besteht aus allen Paaren , für die gilt .
Du kannst dir die Relation auf einer Menge auf zwei Arten bildlich veranschaulichen: wie oben gesehen durch ein Pfeildiagramm, das für jedes Paar der Relation einen Pfeil von nach enthält (links in der untenstehenden Abbildung), oder auch durch einen Graphen, dessen Knoten die Elemente der Menge sind und der eine Kante vom Knoten zum Knoten enthält, wenn das Paar ein Element der Relation ist (rechts in der untenstehenden Abbildung).
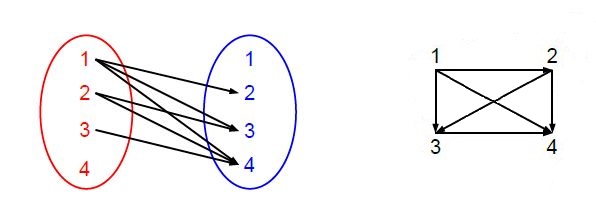
Veranschaulichung einer Relation durch Pfeildiagramm bzw. Graph
Eigenschaften von Relationen
Du kannst Relationen anhand bestimmter Eigenschaften klassifizieren:
Eine Relation auf der Menge heißt
reflexiv, wenn für alle gilt:
symmetrisch, wenn für alle gilt:
asymmetrisch, wenn für alle gilt:
antisymmetrisch, wenn für alle gilt:
transitiv, wenn für alle gilt:
total, wenn für alle gilt:
Beispiele
Zugrundegelegt ist die Menge . Betrachte die Eigenschaften folgender Relationen auf der Menge .
Die Relation ist reflexiv.
Die Relation ist symmetrisch.
Die Relation ist asymmetrisch.
Die Relation ist antisymmetrisch (aber nicht asymmetrisch).
Die Relation ist transitiv.
Die Relation ist total.
Manche Relationen haben gleich mehrere der oben angegebenen Eigenschaften.
Eine Relation, die reflexiv, symmetrisch und transitiv ist, heißt Äquivalenzrelation.
Eine Relation, die reflexiv, antisymmetrisch und transitiv ist, heißt Halbordnung.
Eine Halbordnung, die total ist, heißt (totale oder lineare) Ordnung.
Typische Beispiele sind folgende:
Die Relation auf der Menge der ganzen Zahlen ist eine Äquivalenzrelation. Zwei ganze Zahlen stehen in dieser Relation "ist kongruent modulo ", wenn sie bei ganzzahliger Division durch denselben Rest ergeben. So gilt zum Beispiel , denn beide Zahlen ergeben den Rest 3 bei Division durch 7.
Die Relation ("ist enthalten in") auf der Potenzmenge einer Menge ist eine Halbordnung. Die Relation ist reflexiv, weil jede Menge in sich selbst enthalten ist, sie ist antisymmetrisch, weil wenn in enthalten ist und in , dann gilt . Und sie ist transitiv, denn wenn in enthalten ist und in , dann ist auch in enthalten.
Die Relation ("kleiner oder gleich") auf der Menge der reellen Zahlen ist eine totale Ordnung.
Aufgaben
Laden
Laden
Laden
