Dieser Kurs hat die Koordinatenform einer Ebene zum Thema. Im Kurs lernst du folgende Inhalte:

• Punktprobe mit der Koordinatenform durchführen (I.)

• Spurpunkte der Koordinatenform bestimmen (II.)

• Herleitung der Koordinatenform verstehen (III.)

• Normalenform verstehen (IV.)

• Koordinatenform aus drei Punkten aufstellen (V.)

• Koordinatenform in einfachen Fällen aufstellen (VI.)

• Einfluss der Koeffizienten auf die Lage der Ebene (VII.)

Du benötigst folgendes Vorwissen:

• Skalarprokt

• Vektorprodukt

• Normalenvektor

• Parameterform von Ebenen

Wie man zwischen den verschiedenen Darstellungsformen von Ebenen wechselst, lernst du nicht in diesm Kurs, sondern im nächsten Kapitel: Umwandeln von Ebenendarstellungen.

Aus Gründen der besseren Leserlichkeit werden Vektoren häufig ebenfalls quer geschrieben. Es geht aber immer eindeutig aus dem Textzusammenhang hervor, dass ein Vektor gemeint ist.

[Beispiel: Der Normalenvektor hat die Koordiaten $\vec{n}=(1\mathrm{/}2\mathrm{/}3)\backslash vec\{n\}=(1/2/3)$].

Eine lineare Gleichung mit drei Unbekannten - die Koordinatenform einer Ebene

Eine Alternative zu der Paramterform ist die Koordinatenform. Die Koordinatenform bietet eine Variante zur Darstellung einer Ebene, die im ersten Zugang nicht so anschaulich wirkt. Sie bietet dafür aber insgesamt sehr viele Rechenvorteile.

Im folgenden wird zuerst ein Beispiel für eine Ebenengleichung in Koordinatenform dargestellt. Hier wird der Fokus zuerst nur auf die algebraische Perspektive gelegt. Erst später wird dann im nächsten Unterkapitel die allgemeine Ebenengleichung hergeleitet und vollständig erklärt.

Ein Beispiel für eine Ebenengleichung ist:

Beispiel:

oder auch:

Hier stehen die drei Buchstaben $x_{1}x\_1$, $x_{2}x\_2$ und $x_{3}x\_3$ (bzw. $x,yx,\; y$ und $zz$) für die drei Koordinaten eines Vektors. Wofür die drei Koeffizienten stehen, wird später im nächsten Teilkapitel erklärt. Auch warum diese Gleichung gerade eine Ebene im drei dimensionalen Raum beschreibt, wird erst im nächsten Teilkapitel erklärt. Hier soll die Ebenengleichung in einem ersten Schritt als eine lineare Gleichung mit drei Variablen betrachtet werden.

Lineare Gleichungen mit zwei Variablen kennst du bereits aus der Mittelstufe. Dort taucht schon eine ganz ähnliche Gleichung wie die obige auf, die dir vertraut sein sollte. Denn eine Gerade kann beschrieben werden durch:

Nur durch einfache Äquivalenzumformungen erhälst du hieraus folgende Darstellung:

Ersetzt du nun noch die Bezeichnungen $yy$ durch $x_{2}x\_2$ und $xx$ durch $x_{1}x\_1$, so sieht die dir bekannte Geradengleichung der dir noch unbekannten Ebenengleichung schon sehr ähnlich:

Der einzige Unterschied besteht nun noch darin, dass in der Ebenengleichung noch ein weiterer Summand auftritt. Ihn brauchst du, um vom zwei-Dimensionalen ins drei-Dimensionale zu gelangen.

Sowohl eine lineare Gleichung mit zwei Variablen wie $gg$ als auch eine lineare Gleichung mit drei Variablen wie $EE$ haben unendlich viele Lösungen. Alle Lösungen von $gg$ lassen sich als Punkte im zwei-dimensionalen Koordinatensystem visualisieren. Ebenso lassen sich alle Lösungen von $EE$ als Punkte im dreidimensionalen Raum visualisieren. Beide Gleichungen beschreiben deshalb einmal eine Gerade und einmal eine Ebene, weil alle Lösungen der jeweiligen Gleichung einmal auf einer Geraden und beim anderen Mal auf einer Ebene liegen. Bevor erklärt wird, warum die Lösungen der Gleichung $EE$ alle in einer Ebene liegen, sollst du noch lernen, wie solche Lösungen bestimmt werden können und wie überprüft werden kann, ob ein Zahlentriple eine Lösung ist oder nicht.

Bestimme mindestens drei Lösungen von $gg$

Auf genau die gleiche Weise kannst du auch Lösungen von $EE$ bestimmen: Für zwei Variablen kannst du willkürliche Zahlen festlegen und die Zahl für die dritte Variable kannst du dann einfach durch das Lösen der linearen Gleichung bestimmen.

Bestimme $aa$ in $P(4\mathrm{\mid }4\mathrm{\mid }a)P(4|4|a)$ so, dass P eine Lösung von $E:1\cdot x_1+2\cdot x_2+4\cdot x_3=4E:\; 1\backslash cdot\; x\_1+2\backslash cdot\; x\_2+4\backslash cdot\; x\_3=4$ ist.

Gucke dir nun die beiden Punkte $PP$ und $QQ$ mit $P(2\mathrm{\mid }1\mathrm{\mid }1)P(2|1|1)$ und $Q(2\mathrm{\mid }1\mathrm{\mid }0)Q(2|1|0)$ an. Wenn du die Koordinaten der beiden Punkte jeweils für die Variablen in der Ebenengleichung einsetzt, kanst du überprüfen, ob die Punkte in der Ebene liegen. Die Punkte liegen in der Ebene genau dann, wenn sie eine Lösung der Ebenengleichung sind. Dieses Verfahren nennt man, genauso wie auch bei Geraden, Punktprobe.

Probier es einmal aus!

Liegen $P(2\mathrm{\mid }1\mathrm{\mid }1)P(2|1|1)$ und $Q(2\mathrm{\mid }1\mathrm{\mid }0)Q(2|1|0)$ in $EE$?

Im ersten Fall kommt eine unwahre Aussage heraus ($8\mathrm{\ne }48\backslash neq4$), der Punkt P liegt also nicht in der Ebene. Im zweiten Fall kommt dagegen eine wahre Aussage heraus ($4=44=4$), also liegt der Punkt in der Ebene.

Fazit:

Insgeamt ist es so, dass alle Punkte, die diese Gleichung der Ebene erfüllen, tatsächlich in der Ebene $EE$ liegen. Die Ebene ensteht also durch unendliche viele Punkte, deren Koordinaten alle die Koordinatengleichung erfüllen.

Dieser Zusammenhang wird im folgenden Bild dargestellt: Du siehst drei rote Punkte. Diese Punkte sind die Schnittpunkte der Ebene mit den Koordinatenachsen. Sie heißen Spurpunkte. Ihre Koordinaten sind: $X(4\mathrm{\mid }0\mathrm{\mid }0)X(4|0|0)$, $Y(0\mathrm{\mid }2\mathrm{\mid }0)Y(0|2|0)$ und $Z(0\mathrm{\mid }0\mathrm{\mid }1)Z(0|0|1)$. Wie man sie berechnet, erfährst du im nächsten Absatz. Weiterhin siehst du sehr viele blaue Punkte. Jeder Punkt mit seinen drei Koordinaten ist eine Lösung der Ebenengleichung. Die Ebene ensteht also durch unendlich viele von diesen Punkten. Im Bild sind freilich 'nur' ca. 200 solcher Punkte eingezeichnet:

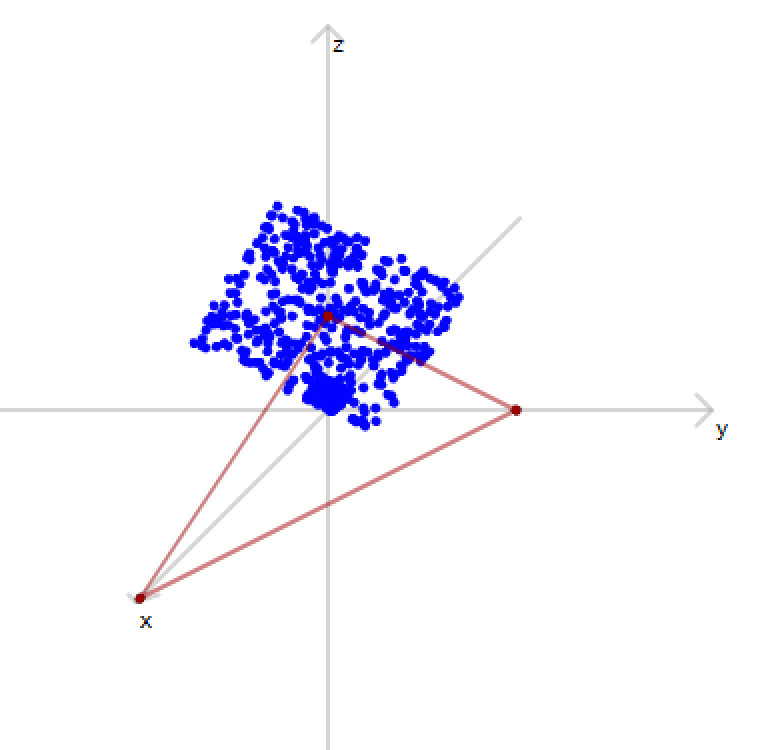
Du kannst dir also eine Ebene in der Koordinatenform gut vorstellen, als eine ebene Punktwolke, deren Punkte so dicht liegen, dass zwischen ihnen kein Platz mehr ist.

Spurpunkte - eine Ebene skizzieren:

Um die zu einer Koordinatengleichung einer Ebene zugehörige Ebene einfach zu visualisieren, nutzt man, genauso wie bei Geraden, ihre Schnittpunkte mit den Koordinatenachsen. Diese Schnittpunkte mit den Koordinatenachsen heißen Spurpunkte. So wie du eine Gerade im KoSy-zeichnen kannst, wenn du ihre beiden Schnittpunkte mit den Koordinatenachsen kennst, so ist es auch bei Ebenen. Der einzige Unterschied ist: hier brauchst du drei Schnittpunkte!

Wenn du schon ahnst, wie es geht, berechne die Spurpunkte der folgenden Ebene:

Die Lösung findest du weiter unten unter Lösung. Wenn du keine Ahnung hast, wie diese Spurpunkte berechnet werden können, lies weiter.

Betrachten wir weiter unsere Ebene aus obigem Beispiel:

Hier stehen die drei Einträge $x_1,x_2\text{und}{x}_{3}x\_1,x\_2\backslash ;\backslash text\{und\}\backslash ;x\_3$ für die drei Koordinatenachsen. Oft werden die drei Achsen statt mit $x_1,x_2\text{und}{x}_{3}x\_1,x\_2\backslash ;\backslash text\{und\}\backslash ;x\_3$ mit $x,y\text{und}zx,\; y\backslash ;\backslash text\{und\}\backslash ;z$ bezeichnet. Dann wird die Ebene aus dem Beispiel so geschrieben:

Welche Schreibweise du vorfindest, hängt also davon ab, wie die Koordinatenachsen beschriftet werden!

Die drei Schnittpunkte mit den Koordinatenachsen haben offensichtlich folgende Gestalt:

Setzen wir den ersten Punkt in die Ebenengleichung ein, so ergibt sich:

$S_{x}inE:1\cdot a+2\cdot 0+4\cdot 0=4S\_x\backslash ;in\backslash ;E:\; 1\backslash cdot\; a+2\backslash cdot\; 0+4\backslash cdot\; 0=4$

Der Schnittpunkt mit der $xx$-Achse ist also $S_x(4\mathrm{\mid }0\mathrm{\mid }0)S\_x(4|0|0)$

Die Schnittpunkte mit den anderen beiden Achsen ermittelt man analog. Berechne die Schnittpunkte mit der $y-y-$ und $z-z-$Achse!

Spurpunkte zum skizzieren der Ebene nutzen

Anschließend zeichnet man diese drei Punkte nun in einem 3-dimensionalen Koordinatensystem ein und verbindet sie:

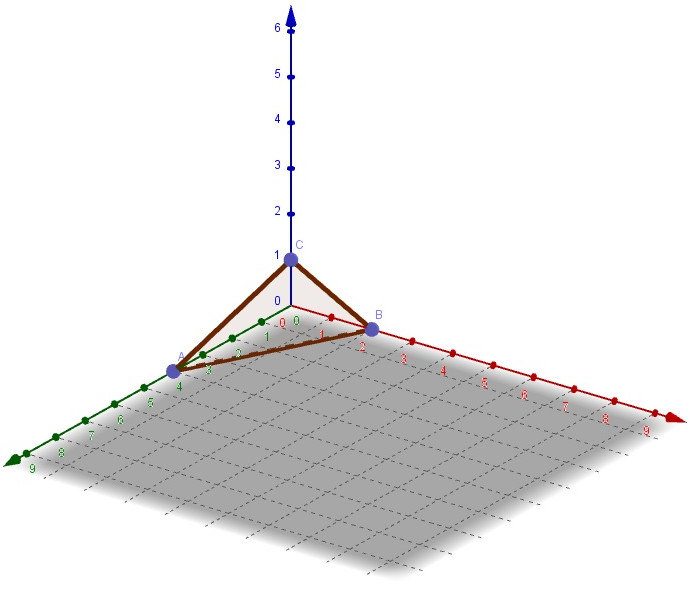
Du siehst an dem Bild, dass z.B. der Punkt $P(5\mathrm{\mid }0\mathrm{\mid }0)P(5|0|0)$ nicht in der Ebene liegt. Dies bestätigt sich auch durch Einsetzen des Punktes in die Koordinatenform:

(unwahre Aussage)

Dagegen kannst du im Bild sehen, dass der Punkt $Q(2\mathrm{\mid }1\mathrm{\mid }0)Q(2|1|0)$ wahrscheinlich in der Ebene liegt. Auch dies bestätigt sich durch Einsetzen des Punktes in die Koordinatenform:

(wahre Aussage)

Die Ebene entsteht durch unendliche viele Punkte und jeder Punkt ist eine Lösung der Gleichung.

Der folgende Link führt dich zu einer LearningApp, bei der du das Gelernte üben kannst:

https://learningapps.org/watch?v=psjeb9bk518

In diesem Kapitel verlagern wir den Standpunkt. Du wirst im folgenden also nicht aus der algebraischen Perspektive auf die Koordinatengleichung einer Ebene gucken, sondern aus einer räumlich-anschaulichen Perspektive von Vektoren. Im nächsten Kapitel werden dann beide Perspektiven miteinander verbunden.

Grundvorstellung:

Stelle dir irgendeine Ebene vor, die auf einem Stützvektor aufliegt. Der Stützvektor fixiert den 'Start' der Ebene. Aber auf diesem Stützvektor kann die Ebene in alle Richungen 'wackeln'. Nun stell dir weiter vor, du würdest senkrecht in diese Ebene einen Vektor als eine Art Griffrohr hineinschrauben. Die Ebene liegt aber immer noch auf dem Stützvektor auf. Mit dem senkrecht auf der Ebene festmontierten Vektor kannst du nun diese Ebene im Raum hin und her bewegen!

Aufgabe:

Baut zusammen mit einfachen Mitteln die eben beschriebene Grundvorstellung in einem Modell nach!Material:

• einen Stift als Stützvektor

• eine Ebene (Handy, kleines Buch …)

• einen Stift als Führungsvektor, der senkrecht auf der Ebene steht (dieser Vektor heißt Normalenvektor)

• ihr definiert irgendwo ein Koordinantensystem (z.B. die Tischkante)

Versucht folgende Aufgaben durch Verwendung eures Modells zu beantworten. Wenn ihr lieber eine Skizze machen wollt, geht das natürlich auch!

Aufgabe 1

Der Stützvektor der Ebene die Koordinaten: $\overrightarrow{OA}=(4\mathrm{/}0\mathrm{/}1)\backslash overrightarrow\{OA\}=\; (4/0/1)$. Damit die Ebene nicht 'wackelt', wird sie von einem Normalenvektor fixiert. Der Normalenvektor hat die Koordinaten $\vec{n}=(5\mathrm{/}0\mathrm{/}0)\backslash vec\{n\}\; =\; (5/0/0)$. Wie liegt die Ebene dann im Raum?

Die visualisierte Lösung der Aufgabe siehst du, wenn du ganz nach unten scrollst!

Aufgabe 2

Auch bei folgender Aufgabe geht es darum, dein Vorstellungsvermögen zu schulen - wie liegt diese Ebene im Raum?

Der Stützvektor ist der Gleiche wie vorhin, also: $\overrightarrow{OA}=(4\mathrm{/}0\mathrm{/}1)\backslash overrightarrow\{OA\}=\; (4/0/1)$. Der Normalenvektor zeigt aber nun parallel in Richtung der z-Achse nach oben. Wie liegt die Ebene dann im Raum?

Aufgabe 3

Fertige eine Skizze der Ebene aus der letzten Aufgabe (Nr.2) an! Zeichne in die Skizze auch einen Stütz- und einen Normalenvektor ein.

Zusammenfassung

Diese Aufgaben hatten die Funktion, dir zu zeigen, dass die beiden Informationen:

• wie gelange ich mit einem Stützvektor vom Ursprung aus zu meiner Ebene ('wo fängt die Ebene an')= Was sind die Koordinaten von $\overrightarrow{OA}\backslash overrightarrow\{OA\}$

• wie genau liegt der Normalenvektor = Was sind die Koordinaten von $\overrightarrow{n}\backslash overrightarrow\{n\}$

ausreichen, um eine Ebene ganz konkret zu definieren!

Wenn dies so ist, muss es doch auch möglich sein, nur mit diesen beiden Informationen algebraisch eine Ebenengleichung aufzustellen!

Dies ist das Ziel des nächsten Kapitels…

Lösung Aufgabe 1

Im folgenden Applett kannst du dir die Ebene aus Aufgabe 1 anschauen. Der Stützvektor ist rot und der Normalenvektor ist schwarz.Du kannst die Ansicht drehen und zoomen.

Mit dem Link kannst du das Applett auch in einem eignen Tab angucken: https://ggbm.at/dnB5FjEc

Jetzt gilt es beide Aspekte zusammenzuführen:

Warum beschreibt eine lineare Gleichung mit drei Variablen eine Ebene? Und welche Rolle spielt dabei die Grundvorstellung, dass ein Normalenvektor und ein Stützvektor ausreichen, um eine Ebene im Raum zu justieren?

Du hast zwei Möglichkeiten Antworten auf diese beiden zentralen Fragen zu bekommen:

1. Möglichkeit

Wenn du abstrakte und kurze mathematische Darstellungen ohne verbale Erklärungen magst, lies das anschließende Unterkapitel IVa.

2. Möglichkeit

Wenn du dagegen ausführliche verbale Darstellungen magst, bei denen viel erklärt wird, lies das übernächste Unterkapitel IVb.

Schau dir die Herleitung im folgenden Applet an!

Dies ist der Link zu folgendem Applett (damit kannst du es größer in einem eignem Tab öffen):

https://ggbm.at/PebnJygJ

Im Applett gibt es eine Taste "Vor", die du immer wieder drücken musst, um Schritt für Schritt durch die Herleitung geführt zu werden.

Allgemeine Form einer Koordinatengleichung:

In der allgemeinen Form der Koordinatengleichung stehen $n_1,n_{2}n\_1,\; n\_2$ und $n_{3}n\_3$ also für die drei Koordinaten des Normalenvektors $\vec{n}=(n_1\mathrm{/}{n}_2\mathrm{/}{n}_3)\backslash vec\{n\}\; =\; (n\_1/n\_2/n\_3)$. Das $x_1,x_{2}x\_1,\; x\_2$ und $x_{3}x\_3$ steht dort als Platzhalter für die drei Koordinaten eines beliebigen Punktes $XX$. Die linke Seite der Gleichung ist also nur das Skalarprodukt vom Normalenvektor und dem Ortsvektor eines x-beliebigen Punktes $XX$:

Das Ergebnis des Skalarproduktes von Normalenvektor und Stützvektor ist eine Zahl - für sie steht im Applet das $dd$.

Also ist die allgemeine Form einer Ebene in Koordinatenform:

Oder, wenn die Zahl $dd$ auf die andere Seite gebracht wird:

Häufig verwendet man auch die dazu äquivalente Schreibweise:

Bei dieser Schreibweise wurden nur die Koordinaten des beliebigen Punktes $XX$, der in der Ebene liegt, umbenannt von $x_1,x_{2}x\_1,\; x\_2$ und $x_{3}x\_3$ in $x,yx,y$ und $zz$.

Eine Koordinatenform aufzustellen, wenn du den Stützvektor und den Normalenvektor kennst, ist also ganz einfach!

• Berechne $dd$ mit dem Skalarprodukt von Stütz- und Normalenvektor

• Setze die Koordinaten des Normalenvektors für $n_1,n_{2}n\_1,\; n\_2$ und $n_{3}n\_3$ ein.

Fertig ;-)

Ein einfaches BeispielSei A mit $(2\mathrm{/}3\mathrm{/}4)(2/3/4)$ ein Punkt in einer Ebene und $\overrightarrow{OA}\backslash overrightarrow\{OA\}$ sei somit der Stützvektor der Ebene. Weiterhin sei $\vec{n}=(3\mathrm{/}1\mathrm{/}4)\backslash vec\{n\}\; =\; (3/1/4)$ ein Normalenvektor der Ebene.

Abschließende Aufgabe:Unter folgendem Link kannst du noch einmal testen, ob du die Herleitung verstanden hast, indem du die einzelnen Begründungsschritte in die richtige Reihenfolge bringst:

https://learningapps.org/21633860

Herleitung der allgemeinen Koordinatenform

Bisher wurde im ersten Kapitel erklärt, das alle Punkte mit 3 Koordinaten, die jeweils eine Lösung einer Koordinatengleichung sind, in einer Ebene liegen. Im zweiten Kapitel hast du gesehen, dass die Lage einer Ebene im Raum eindeutig durch die Angabe eines Stützvektors und eines Normalenvektors definiert ist. Nun werden beide Aspekte zusammengebracht und du lernst, warum die allgemeine Koordinatenform eine Ebene beschreibt.

Im Applet unten siehst du eine Ebene, die von einem Stützvektor angesteuert. Dieser Stützvektor ist in der Abbildung rot dargestellt.Ihn kennst du aus der Parameterdarstellung einer Ebene. Ohne ihn kann auch keine Koordinatenform gebildet werden.

Neu in der Darstellung sind jedoch der grüne Vektor und der orangene Vektor. Der grüne Vektor steht senkrecht auf der Ebene und heißt Normalenvektor. Jeder Vektor, der in der Ebene liegt, steht senkrecht zum grünen Normalenvektor $\vec{n}\backslash vec\{n\}$. Der orange Vektor dagegen verbindet den Punkt A, der das Pfeilende vom Stützvektor ist, mit jedem x-beliebigen Punkt X in der Ebene. Er heißt also $\overrightarrow{AX}\backslash overrightarrow\{AX\}$:

Du kannst im Applet den Punkt X an jede x-beliebige Stelle verschieben. Welche Beziehung wird jedoch immer zwischen dem grünen Normalenvektor $\vec{n}\backslash vec\{n\}$ und dem orangenen Vektor $\overrightarrow{AX}\backslash overrightarrow\{AX\}$ bestehen?

Wenn $\overrightarrow{AX}\backslash overrightarrow\{AX\}$ und $\vec{n}\backslash vec\{n\}$ immer - also unabhängig von der Lage des Punktes X in der Ebene - senkrecht zueinander stehen, heißt das algebraisch, dass ihr Skalarprodukt immer Null ist.

Stell dir vor, der Punkt X würde nicht mehr in der Ebene liegen, sondern ein Stückchen über oder unter ihr. Dann würde der orangene Vektor auch nicht mehr senkrecht zum grünen Vektor sein. Dann wäre ihr Skalarprodukt auch nicht mehr Null.

Nun geht es darum, den soeben beschriebenen Zusammenhang algebraisch zu formulieren, um die Koordinatenform einer Ebene herzuleiten.

Zuerst überlegen wir uns, wie der orangene Vektor berechnet werden kann. Er führt vom Punkt A, der Pfeilspitze des Stützvektors, zu einem x-beliebigem Punkt X in der Ebene. Er kann für jeden beliebigen Punkt berechnet werden durch:

Oben hast du gesehen, dass der orangene Vektor zum grünen Normalenvektor senkrecht steht. Also gilt:

Diese Gleichung besagt: Das Skalarprodukt von Stützvektor mit einem Vektor, der zwischen einem Punkt A in der Ebene und irgendeinem beliegiem anderen Punkt in der Ebene geht, ist Null.

Um nun zu der Koordinatenform zu gelangen, müssen wir nur noch algebraische Umformungen vornehmen.

Zuerst wird das Distributivgesetz angewandt, um die Klammer aufzulösen:

Danach können wir den rechten Summanden auf die andere Seite der Gleichung bringen:

Nun multipliziert man beide Seiten der Gleichungen nach der Definition des Skalarproduktes aus:

Auf der linken Seite der Gleichung steht also das Skalarprodukt eines Vektor $\overrightarrow{OX}\backslash overrightarrow\{OX\}$ mit einem Normalenvektor $\vec{n}\backslash vec\{n\}$. $\overrightarrow{OX}\backslash overrightarrow\{OX\}$ ist ein Ortsvektor zu irgeneinem beliebigen Punkt in der Ebene, den wir nicht kennen. Der Normalenvektor $\vec{n}\backslash vec\{n\}$ ist der senkrecht auf der Ebene stehende Vektor, dessen Koordinaten bekannt sein müssen.

Auf der rechten Seite der Gleichung steht das Skalarprodukte eines Vektors $\overrightarrow{OA}\backslash overrightarrow\{OA\}$ mit dem Normalenvektor $\vec{n}\backslash vec\{n\}$. Beide Vektoren müssen ebenfalls bekannt sein. Weil beide Vektoren bekannt ist, ist das Ergebnis dieses Skalarpoduktes eine Zahl, für die man auch einfach $dd$ schreiben kann:

Allgemeine Form einer Koordinatengleichung:

häufig verwendet man auch die dazu äquivalente Schreibweise:

In dieser Form stehen die drei Buchstaben $n_1,n_2,n_{3}n\_1,\; n\_2,n\_3$ für die drei Koordinaten des Normalenvektors $\vec{n}\backslash vec\{n\}$. Er ist in der Regel bekannt. Die drei Buchstaben $x_1,x_2,x_{3}x\_1,x\_2,x\_3$ (oder auch $x,y,zx,y,z$) stehen für die drei Koordinaten eines beliebigen und unbekannten Vektors $\vec{x}\backslash vec\{x\}$. Der Buchstabe $dd$ auf der rechten Seite ist das Ergebnis des Skalarproduktes eines bekannten Stützvektors der Ebene $\overrightarrow{OA}\backslash vec\{OA\}$ mit dem Normalenvektor.

Schau dir noch einmal das obige Geogebra-Applet an. Dort ist grüne Normalenvektor $\vec{n}\backslash vec\{n\}$=(0/0/1). Der rote Stütz-Vektor $\overrightarrow{OA}\backslash vec\{OA\}$ hat die Koorinaten (1/1/1). Also ist eine Koordinatenform der Ebene:

also lautet die Ebenegleichung zu der Ebene im Applet:

Ein einfaches BeispielSei A mit $(2\mathrm{/}3\mathrm{/}4)(2/3/4)$ ein Punkt in einer Ebene und $\overrightarrow{OA}\backslash overrightarrow\{OA\}$ sei somit der Stützvektor der Ebene. Weiterhin sei $\vec{n}=(3\mathrm{/}1\mathrm{/}4)\backslash vec\{n\}\; =\; (3/1/4)$ ein Normalenvektor der Ebene.

Abschließende Aufgabe:Unter folgendem Link kannst du noch einmal testen, ob du die Herleitung verstanden hast, indem du die einzelnen Begründungsschritte in die richtige Reihenfolge bringst:

https://learningapps.org/21633860

Während der obigen Herleitung war die zentrale Überlegung, dass das Skalarprodukt jedes Normalenvektors einer Ebene mit dem Vektor, der einen x-beliebigen Punkt der Ebene mit dem Stützvektor verbindet, Null sein muss. Diese Überlegung wird durch folgende Gleichung ausgedrückt:

Da sie so zentral ist, erhält sie so wie die Koordinatenform einen eigenen Namen. Sie heißt Normalform und ist eine weitere Darstellungsform einer Ebene. Bei der Normalform spannt der Normalvektor $\vec{n}\backslash vec\{n\}$ und ein Aufpunkt $\vec{A}\backslash vec\{A\}$ die Ebene auf, das Skalarprodukt wird jedoch nicht (mit Distributivgesetz) aufgelöst. (Oder, wenn du von der Koordinatenform aus guckst,ist der Unterschied, dass der Normalenvektor $\vec{n}\backslash vec\{n\}$ sozusagen ausgeklammert wurde.)

Beispielaufgaben

1.Aufgabe

Wandle folgende Normalenform in eine Koordinatenform um:$\mathrm{E}:\left(\begin{array}{c}6\\ -1\\ -4\end{array}\right)\circ [\left(\begin{array}{c}{\mathrm{x}}_1\\ {\mathrm{x}}_2\\ {\mathrm{x}}_3\end{array}\right)-\left(\begin{array}{c}1\\ 0\\ 3\end{array}\right)]=0\backslash mathrm\; E:\backslash ;\backslash begin\{pmatrix\}6\backslash \backslash -1\backslash \backslash -4\backslash end\{pmatrix\}\backslash circ\backslash left[\backslash begin\{pmatrix\}\{\backslash mathrm\; x\}\_1\backslash \backslash \{\backslash mathrm\; x\}\_2\backslash \backslash \{\backslash mathrm\; x\}\_3\backslash end\{pmatrix\}-\backslash begin\{pmatrix\}1\backslash \backslash 0\backslash \backslash 3\backslash end\{pmatrix\}\backslash right]=0$

2.Aufgabe

Gegeben ist ein Punkt $P(3\mathrm{/}8\mathrm{/}-1)P\; (3/8/-1)$ und ein Vektor $\vec{n}=(-4\mathrm{/}2\mathrm{/}1)\backslash vec\{n\}\; =\; (-4/2/1)$ Stelle eine Normalenform auf.

3.AufgabeNun der umgekehrte Weg. Gegeben ist folgende Koordinatenform:

Forme um, in die Normalenform:

Koordinatenform aus drei Punkten ermitteln

Im ersten Beispiel hatten wir folgenden Koordinatenform:

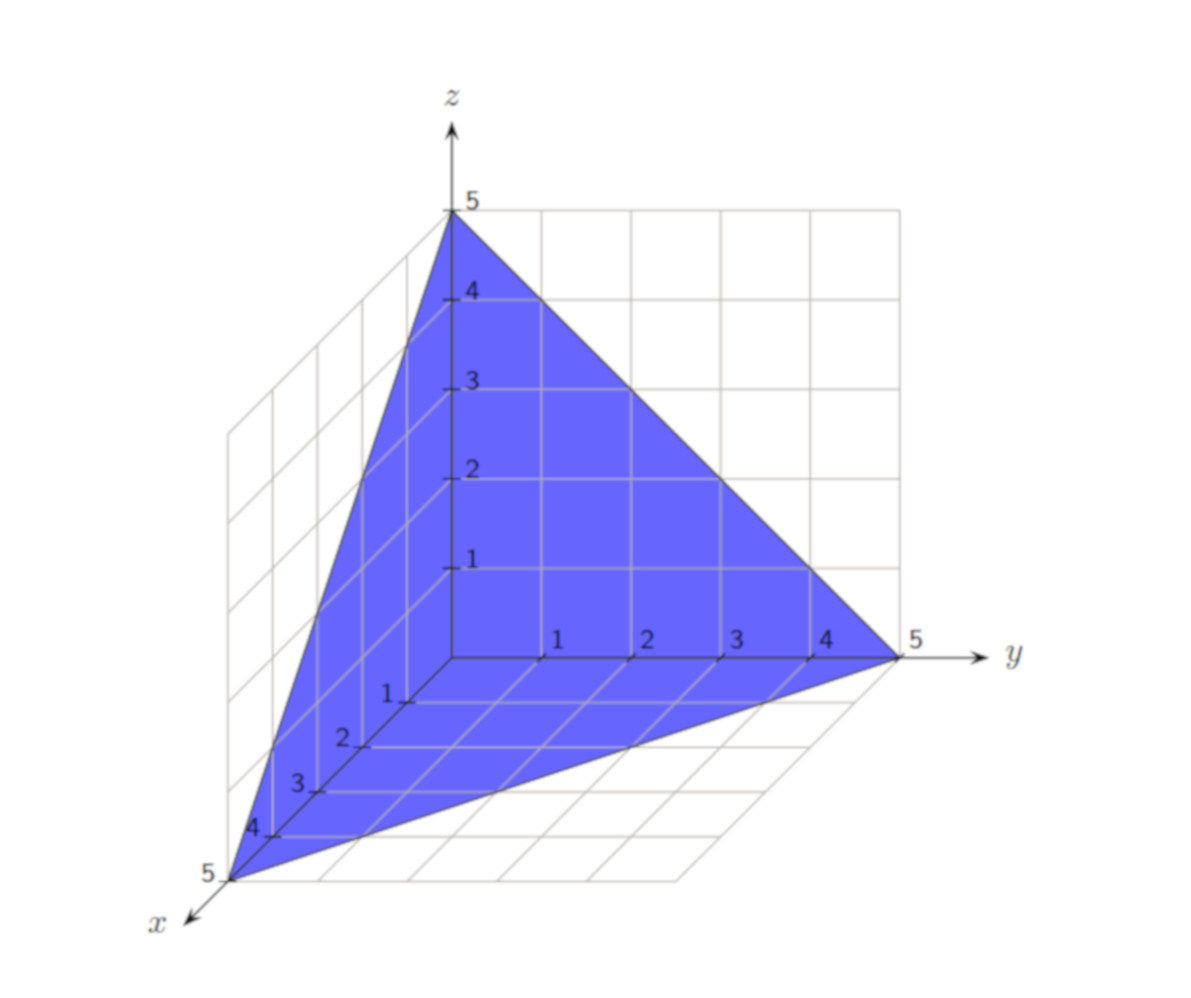
Der Ausschnitt der Ebene, der im 1.Quadranten liegt, sieht so aus:

Nun nimm an, du wüßtest nicht, wie die Ebenengleichung lautet und überlege kurz: Wie kannst du eine solche Gleichung aufstellen, wenn du nur die Koordinaten der drei Punkte A, B und C kennst?A(4/0/0)B(0/2/0)C(0/0/1)

Aufgabe: Notiere einen Ansatz!

Aufgabe: Führe den Ansatz mit den Werten von A, B und C aus!

Ein Stützvektor der Ebene ist der Vektor $\overrightarrow{OA}\backslash vec\{OA\}$mit (4/0/0). Der Normalenvektor der Ebene muss auf orthogonal auf der Ebene stehen, er muss als auch orthogonal zu beiden Spannvektoren sein. Als Spannvektoren können wir hier gut die Vektoren $\overrightarrow{AC}\backslash vec\{AC\}$ mit (-4/0/1) und $\overrightarrow{BC}\backslash vec\{BC\}$ mit (0/-2/1) wählen. Der Normalenvektor wird mit dem Vektorprodukt bestimmt und ist: $\vec{n}\backslash vec\{n\}$ = (2/4/8).

Das Skalarprodukt von Stützvektor und Normalenvektor ist hier:

Also lautet eine Ebenengleichung:

Vergleiche mal $E_{1}E\_1$ und die Gleichung $E_{2}E\_2$!

Beide Ebenengleichungen unterscheiden sich nur um den Faktor 2. Offensichtlich gelten für die Koordinatenform die gleichen Rechengesetzte wie für Gleichungen.

Eine Ebene in Koordinatenform hat also unendlich viele Darstellungsmöglichkeiten, die sich nur durch Äquivalenzumformungen unterscheiden.

Multipliziere mal $E_{1}E\_1$ mit 32!

Dies ist aber auch logisch, denn der Normalenvektor einer Ebene hat ja keine vorgegebene Länge. Der Normalenvektor von $E_{1}E\_1$ ist $\overrightarrow{n_1}\backslash vec\{n\_1\}$=(1/2/4) und der Normalenvektor von $E_{2}E\_2$ ist $\overrightarrow{n_2}\backslash vec\{n\_2\}$=(2/4/8). Da der eine Vektor ein Vielfaches des anderen Vektors ist, unterscheiden sich beide Vektoren auch nur in der Länge! Auch der Vektor $\overrightarrow{n_3}\backslash vec\{n\_3\}$=(-4/-8/-16) ist ein Normalenvektor der Ebene. Er ist nur drei mal so lang und zeigt in die andere Richtung. Mit ihm kann auch wieder eine Ebenegleichung für die gleiche Ebene aufgestellt werden. Dazu muss er skalar mit einem Stützvektor multipliziert werden. In der Darstellung oben ist zu sehen, dass auch $\overrightarrow{OB}\backslash vec\{OB\}$ =(0/2/0) so ein Stützvektor ist. Also gilt:

Also ist eine vierte Gleichung der Ebene E:

Nun also eine kleine Übung zum Ermitteln einer Koordinatenform aus drei Punkten. Nimm einen Stift und stelle zu den folgenden drei Punkten eine Koordinatengleichung auf und überprüfe dein Ergebnis: Punkten aufstellen

Eine Koordinatenform aus einer Darstellung ermitteln

Schau dir foglgenden Ausschnitt einer Ebene an und überlege, wie du eine Ebenengleichung aufstellen kannst:

Hier soll nun ein anderer Weg gewählt werden. Überlege, ob dir noch ein anderer Weg einfällt, bei dem du keinen Normalenvektor zu berechnen brauchst!

Für diese Ebene gilt also:

Du kannst mit folgenden Links das Ermitteln einer Koordinatenform üben:

https://learningapps.org/watch?v=p026g1uzn18

https://learningapps.org/watch?v=purt9o92518

Wenn du noch Hilfe brauchst, kannst du dir in einem Erklärvideo noch einmal angucken, wie in einfachen Fällen zu einer gegebenen Ebene in einem Koordinatensystem eine Koordinatenform aufgestellt werden kann:

https://youtu.be/h116QoLFK0o

Hier findest du einige Links zu Aufgaben, die bei Geogebra hinterlegt sind. Alle diese Aufgaben behandeln Ebenenscharen und entsprechen somit nicht mehr den typischen Aufgaben zu diesem Themengebiet, die in einem Grundkurs zu finden sind.

• Aufgabe: parallele Ebenen bei der Koordinatenform https://ggbm.at/MKSTRfwJ

• Aufgabe: Spurpunkte einer Ebenenschar https://ggbm.at/tTkDXDPF

• Aufgabe: Ebenenschar Ea: 4x+2y-3z = 4a https://ggbm.at/AqVERPSg