Ein 3-dimensionales Objekt lässt sich nicht auf einem 2-dimensionalen Blatt Papier abbilden. Doch durch eine Schrägzeichnung scheint ein 3-dimensionales Objekt Tiefe zu besitzen, indem die nach vorne bzw. hinten verlaufenden Strecken schräg gezeichnet werden.
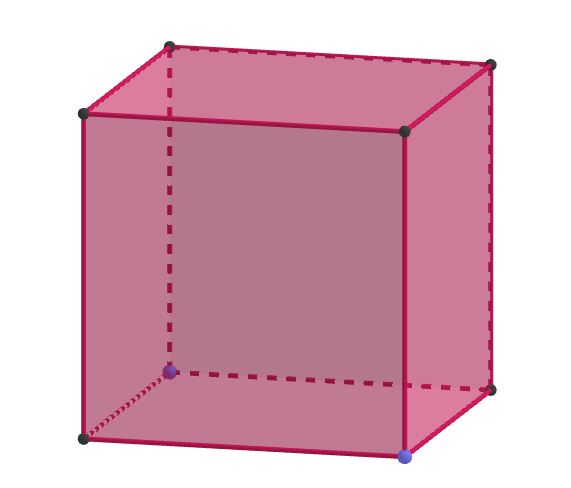
Allgemeine Konstruktion
Für jeden 3-dimensionalen Körper verläuft die Schrägbildkonstruktion etwas anders. Hier soll eine allgemeine Konstruktion eines Würfels bzw. Quaders und einer Pyramide zeigen, welche Schritte gleich bzw. unterschiedlich ablaufen.
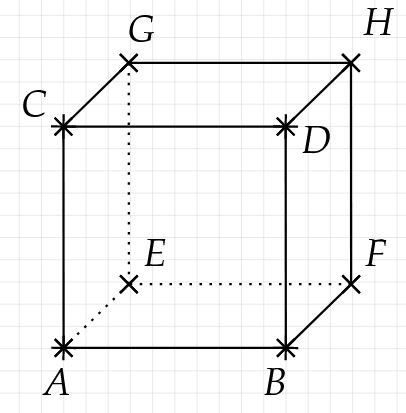
Würfel/Quader im Schrägbild zeichnen
Zeichne die Grundlinie des Würfels/Quaders, diese besitzt die Länge der vorgegebenen Kantenlänge (hier Längeneinheiten).
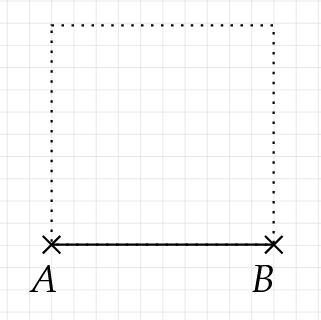
Vervollständige die Vorderseite des Würfels/Quaders. Die Beschriftung scheint etwas willkürlich zu sein, aber die Punkte sollten nicht über den schrägen Strecken liegen.
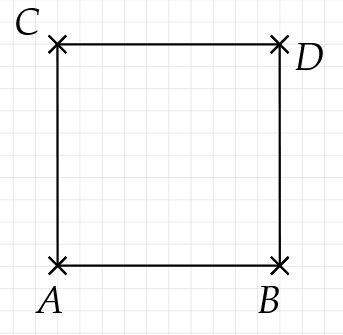
Die von nach hinten verlaufende Strecke wird schräg in einem Winkel zur Horizontalen gezeichnet.
Hier soll der Maßstab betragen. Das heißt, die Strecke wird halb so lang gezeichnet, als sie eigentlich ist. Vorsicht: Die Hälfte von Kästchen wären nicht Kästchendiagonalen. Die Strecke muss am Geodreieck abgemessen werden.
Zeichne die Schrägen an alle Ecken der Vorderseite.
Strecken, die eigentlich nicht aus dieser Ansicht sichtbar wären, werden gestrichelt.
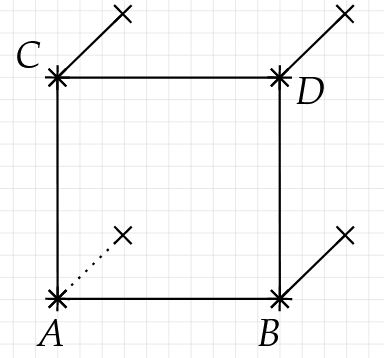
Vervollständige die Zeichnung mit den fehlenden Strecken und der Beschriftung.
Pyramiden im Schrägbild zeichnen
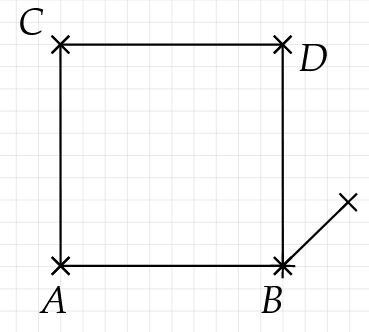
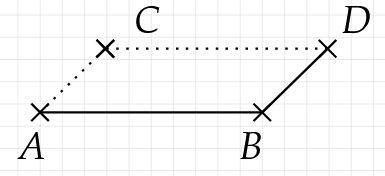
Zeichne die Grundlinie der Pyramide, diese besitzt eine vorgegebene Kantenlänge (hier Längeneinheiten) und befindet sich an der vorderen Seite der Grundfläche.
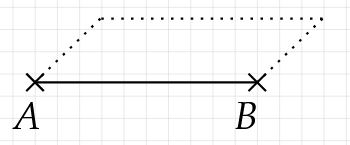
Von bzw. aus, zeichne die Schräge zu den Punkten und .
Achte darauf, Strecken gestrichelt zu zeichnen, wenn sie in der Ansicht des Körpers eigentlich nicht von vorne zu sehen sind.
Der Winkel zur Horizontalen und der Maßstab der Schrägen müssen vorgegeben sein, ansonsten wird der Winkel und der Maßstab verwendet.
Verbinde die Punkte und , sowie und , um die Diagonalen der Grundfläche zu erhalten. Diese sind Hilfslinien für den nächsten Schritt.
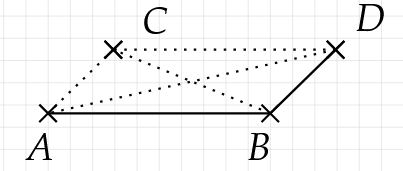
Die Spitze der Pyramide befindet sich in einer vorgegebenen Höhe über der Grundfläche. Diese Höhe wird als Hilfslinie senkrecht nach oben gezeichnet.
Der Schnittpunkt der Diagonalen bildet hier den Anfang, da dieser mittig in der Grundfläche liegt.
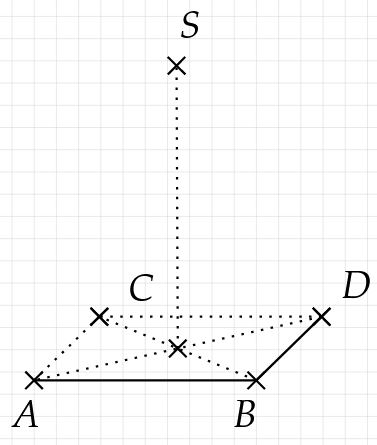
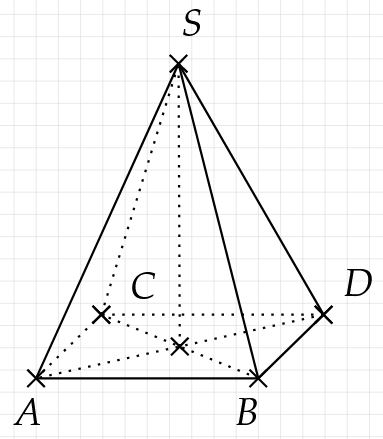
Verbinde die verbleibenden Strecken. Achte darauf, Strecken gestrichelt zu zeichnen, wenn sie aus dieser Ansicht eigentlich nicht gesehen werden können.
Winkel und Maßstab der Schrägen
Der Winkel, in dem die schrägen Strecken der Zeichnung verlaufen, muss, wie auch der Maßstab dieser Strecke, vorgegeben sein. Es gibt keine Faustformel, außer für definierte Ansichten, wie es bei technischen Zeichnungen der Fall ist. Es gilt:
Der Maßstab wird zur Berechnung der Länge der Strecke verwendet.
Hat eine Strecke die tatsächliche Länge , hat sie bei einem Maßstab die Länge in der Zeichnung.
Applet: Konstruktion eines beliebigen Quaders
Zeichne zuerst nur eine Vorderseite der Figur.
Zeichne an eine Ecke eine Strecke, die mit der Waagrechten einen Winkel kleiner als einschließt. Der Winkel sollte nach Möglichkeit auch nicht sein.
Zeichne an die anderen Ecken die gleiche Strecke ein.
Verbinde nun die Streckenenden. Es muss die Figur herauskommen, mit der man angefangen hat.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
