Das Haus der Vierecke sortiert die verschiedenen Vierecksarten nach ihren Eigenschaften.
Dabei hat ein Viereck in einem höheren Stockwerk im Haus mehr besondere Eigenschaften als die Vierecke in den niedrigeren Etagen.
Ist ein Viereck über einem (oder mehreren) anderen zu finden, so hat er alle Eigenschaften von seinem unteren Nachbarn und noch mehr.
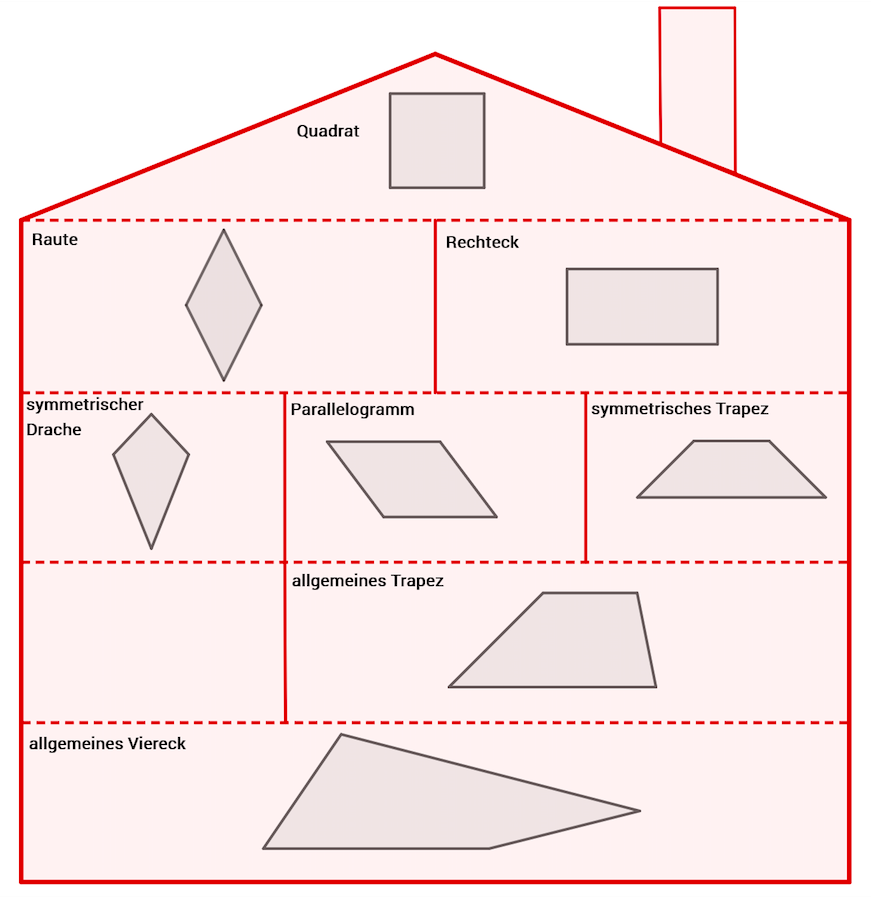
Ein Beispiel zum Hausaufbau:
Ein Rechteck ist immer auch ein symmetrisches Trapez.
Ein Quadrat ist immer auch ein Drachenviereck.
Ein Rechteck ist nicht immer ein Quadrat!
Zusammenhang zwischen den Vierecken
Das Haus der Vierecke ordnet die verschiedenen Vierecksarten nach Kriterien wie Symmetrie, Winkelbeziehungen und Seitenbeziehungen im Viereck. Weiß man zum Beispiel, dass ein "Elternteil" achsensymmetrisch zu einer seiner Diagonalen ist, so wird diese Eigenschaft auch an das "Kind" weitergegeben und das neue Viereck ist ebenfalls symmetrisch zu seiner Diagonalen. Dadurch kann man nun die Eigenschaften der in den einzelnen Artikeln vorgestellten Vierecke übersichtlich darstellen
Symmetrien
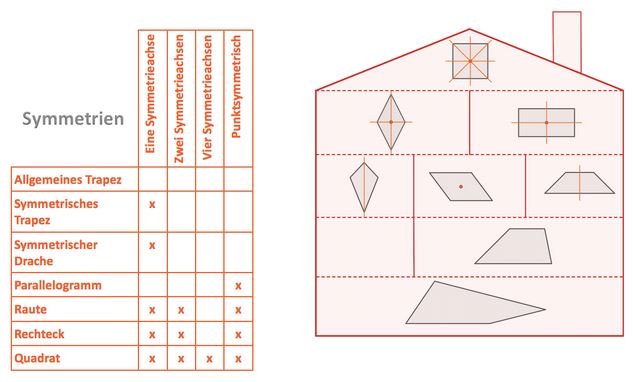
Winkelbeziehungen
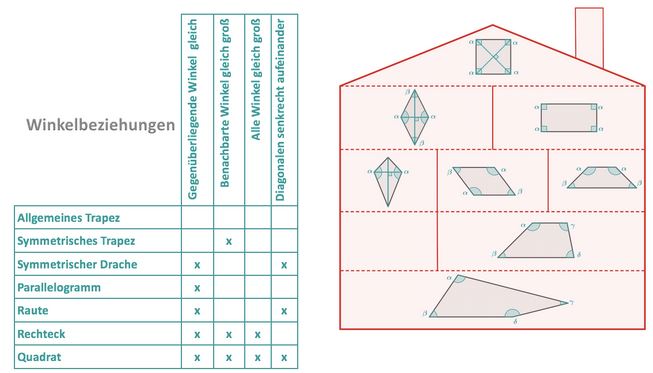
Seitenbeziehungen
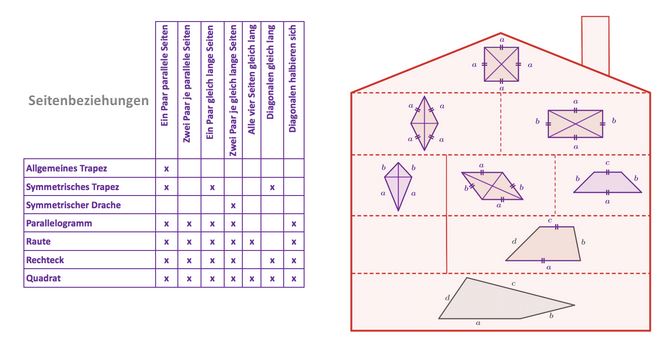
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Beziehungen zwischen den besonderen Vierecksarten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
