1 Übersicht
In diesem Kurs lernst du die Linsengleichung oder auch Abbildungsgleichung kennen, mit der man Linsen auswählen kann, damit von der Brille bis zum Teleskop scharfe Bilder erzeugt werden können.
Vorwissen
Geometrische Bestimmung der Bildgröße und Bildweite
Kursdauer
ca. 30 min
2 Einführung
Linsen sind dir schon bekannt. Du kennst Sammellinsen (konvex) und Zerstreuungslinsen (konkav). Wie groß das Bild eines Gegenstandes ist, hast du über eine Zeichnung bestimmt. Die Brennpunkte F1 und F2 befinden sich auf der gestrichelten optischen Achse im Abstand f zur Mitte der Linse.
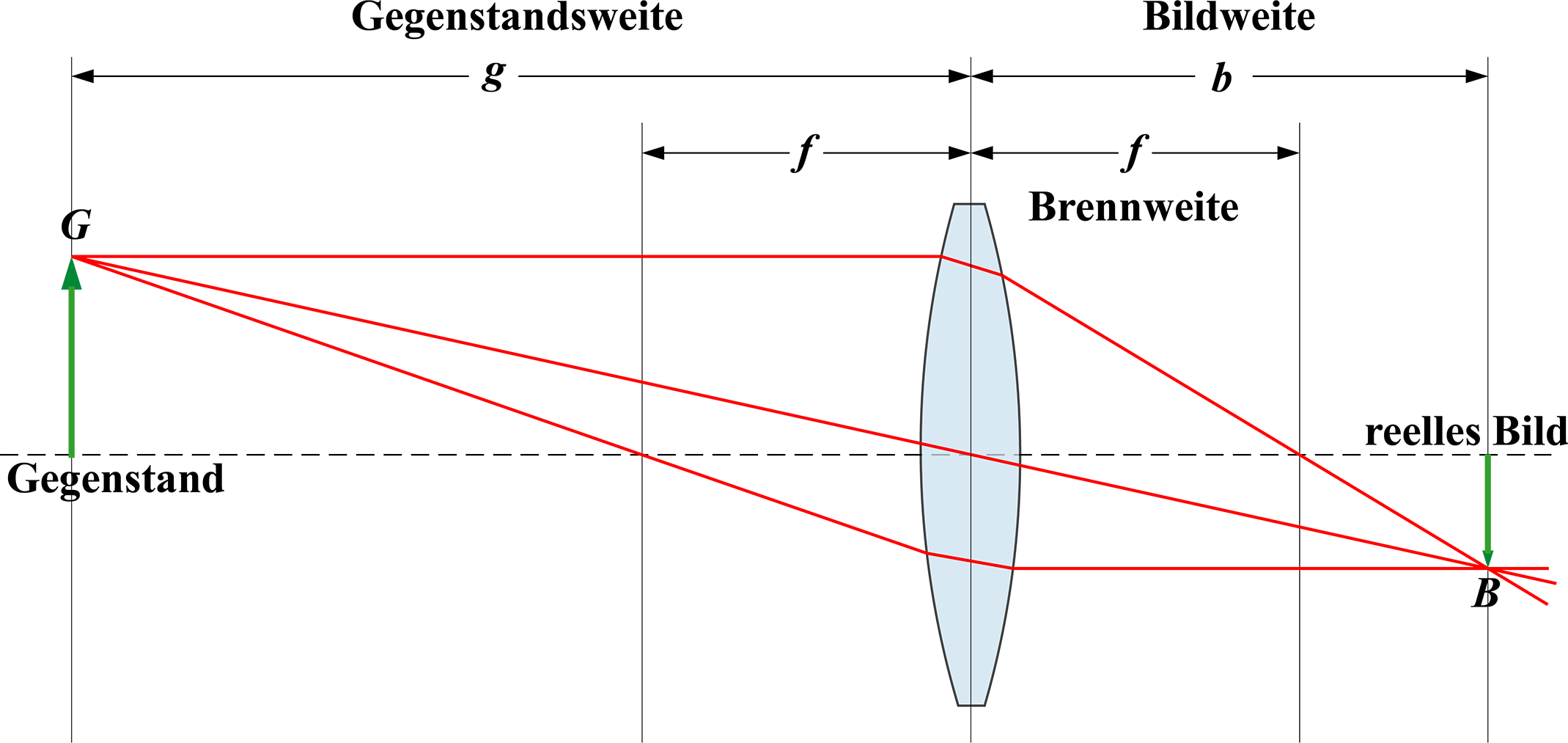
Bildquelle: Anastasius zwerg, CC BY-SA 3.0, Wikimedia
Du siehst von oben nach unten die drei roten Strahlen
Parallelstrahl (parallel bis zur Linse, dann durch den Brennpunkt F2)
Mittelpunktstrahl (Halbgerade durch den Mittelpunkt der Linse)
Brennpunktstrahl (zuerst durch den Brennpunkt F1 bis zur Linse, dann parallel zur optischen Achse weiter)
Alle drei schneiden sich in einem Punkt, wo die Spitze des Bildes entsteht. Für die zeichnerische Konstruktion würden also zwei Strahlen reichen.
3 Bildentstehung
Bei einer Sammellinse entsteht das Bild durch den Schnittpunkt der drei besonderen Strahlen. Aber nicht nur für diese Strahlen gilt das. Alle von der Spitze des Gegenstandes ausgehenden Strahlen schneiden sich in der Spitze des Bildes. Klicke in der Simulation unten auf „Show many rays“ (Zeige viele Strahlen) und bewege die Spitze des Gegenstandes. Mit Strg+Mausrad auf eine Stelle außerhalb der Simulation kannst du das schwarze Fenster größer machen.
Du erinnert dich vielleicht an eine weitere Eigenschaft von Sammellinsen: Lichtstrahlen, die parallel zur optischen Achse verlaufen, gehen hinter der Linse alle durch den Brennpunkt F. Das erklärt den Verlauf des Parallelstrahls.
Den geometrischen Zusammenhang hast du jetzt wiederholt. Nun wollen wir Formeln finden, um die Größen miteinander zu verbinden und sie zu berechnen.
4 Linsengleichung
Das Bild vom Anfang hilft dir auf dem Weg zur Linsengleichung.

Bildquelle: Anastasius zwerg, CC BY-SA 3.0, Wikimedia
Mach dir die Bezeichnungen nochmal klar:
Gegenstandsgröße G
Gegenstandsweite g
Bildgröße B
Bildweite b
Brennweite f
Der Gegenstand ist links von der Linse, das Bild im Normalfall rechts von ihr.
„...größen“ gehen von oben nach unten; „...weiten“ gehen von links nach rechts. Alles wird wie für Längen üblich immer in Metern gemessen, z.B. G=0,45 m.
In einer weiteren Simulation nähern wir uns der gesuchten Formel. Wir untersuchen den Zusammenhang zwischen g, b und f. Wenn man die Werte miteinander vergleicht, wird man kein Muster erkennen. Allerdings passiert etwas Interessantes, wenn man die Kehrwerte der Größen betrachtet.
In dieser Simulation kannst du mit drei Größen spielen:
G am Schieberegler
g durch den unteren Punkt von G auf der optischen Achse
f durch die Position von F2 auf der optischen Achse
Bemerkung: Die Simulation lässt der Einfachheit halber die Einheiten weg. Alle Zahlen hätten die Einheit .
Egal, wie man diese Größen wählt. Du siehst:
Wenn man G, g und f vorgibt, sind B und b eindeutig festgelegt.
Die Kehrwerte von g und b addieren sich zum Kehrwert von f.
Die zweite Erkenntnis gießen wir in eine Formel:
Diese Gleichung nennen wir Linsengleichung und geben ihr die Nummer (1), da wir sie nochmal benötigen. Das war keine mathematische Herleitung und kein Beweis, wir haben bisher nur die Vermutung anhand der Zahlen, dass die Formel stimmt. Auf der nächsten Seite wollen wir die Formel herleiten. Und wir haben uns noch keine Gedanken zur Berechnung von B gemacht.
5 Herleitung der Formeln
Die Herleitung der Linsengleichung und eine Formel für B ist einfacher, als du denkst. Es wird der Strahlensatz verwendet, den du schon kennst. Alles weitere sind nur Umformungen.
In dieser Simulation kannst du dir die Dreiecke "M" mit M in der Mitte und die Dreiecke "F" mit F in der Mitte anzeigen. Aktiviere zuerst bitte die zwei grünen Dreiecke "M".
Die Strahlensätze darf man hier anwenden, weil G und B parallel sind.
Eine Gleichung für B erhalten wir sofort durch den 2. Strahlensatz:
Das ist Gleichung Nummer (2). Jetzt solltest du die zwei violetten Dreiecke "F" aktivieren. Mach dir klar, dass der Abstand von F2 zum Punkt von B auf der optischen Achse b-f beträgt. Jetzt benutzen wir in den violetten Dreiecken den 2. Strahlensatz:
| ↓ | Die linke Seite wird durch Gleichung (2) ersetzt. | ||
| ↓ | Die rechte Seite wird umgeformt. | ||
| ↓ | ( kann ja nicht Null sein) | ||
| ↓ | Das ist Gleichung (1). | ||
Du hast es geschafft!
Mit der Kombination der beiden Formeln und kann man die beteiligten Größen bei der Sammellinse berechnen.
Das üben wir nun in einer Aufgabe. Aber zuerst darfst du noch mit einer Katze und ihrem Bild herumspielen.
Laden
6 Aufgabe zur Linsengleichung
Um das Gelernte zu üben, bearbeite folgende Aufgabe:
Laden
