a)
(3 BE)
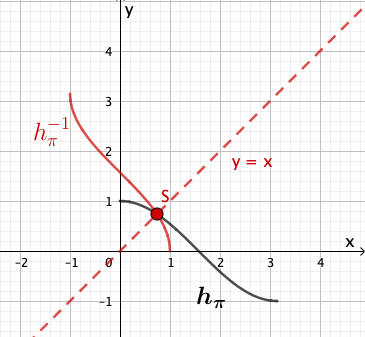
Betrachtet wird eine Schar von Funktionen mit , die sich nur in ihren jeweiligen Definitionsbereichen unterscheiden.
Es gilt mit .
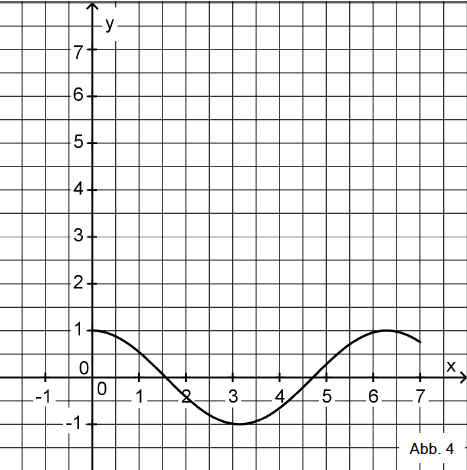
Abbildung 4 zeigt den Graphen der Funktion . Geben Sie den größtmöglichen Wert von an, sodass die zugehörige Funktion umkehrbar ist. Zeichnen Sie für diesen Wert von den Graphen der Umkehrfunktion von in Abbildung 4 ein und berücksichtigen Sie dabei insbesondere den Schnittpunkt der Graphen von Funktion und Umkehrfunktion.
b)
(2 BE)
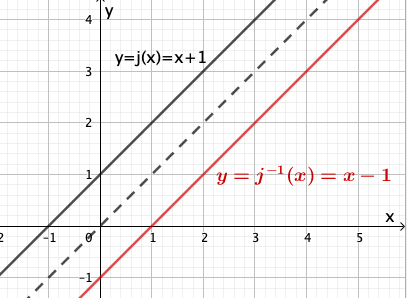
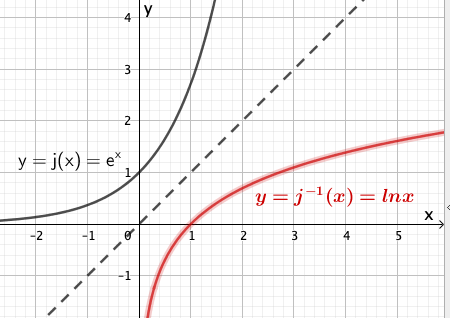
Geben Sie den Term einer in definierten und umkehrbaren Funktion an, die folgende Bedingung erfüllt: Der Graph von und der Graph der Umkehrfunktion von haben keinen gemeinsamen Punkt.