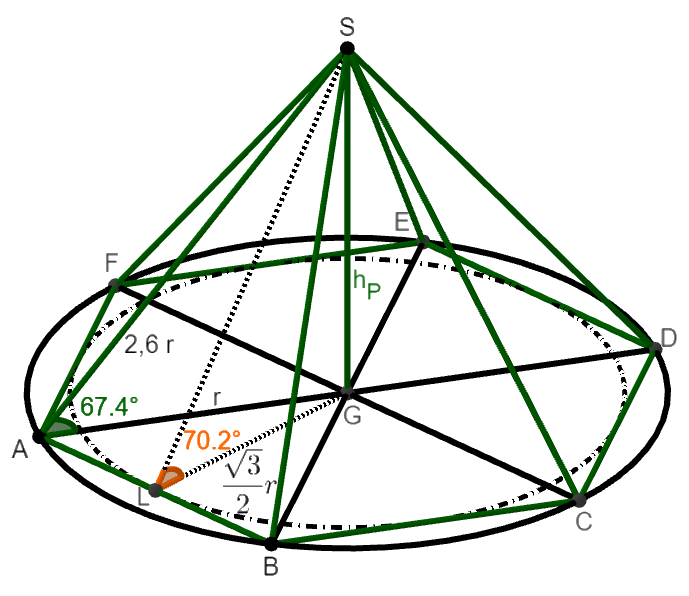
Eine Pyramide habe als Grundfläche ein regelmäßiges Sechseck mit Umkreisradius ( Grundkantenlänge auch und der Inkreisradius ist ).
Der Höhenfußpunkt der Pyramide ist der Umkreismittelpunkt, die Seitenkantenlänge ist .
Berechne das Volumen der Pyramide.
Berechne den Neigungswinkel der Seitenkante zur Grundfläche und den Neigungswinkel der Seitenfläche zur Grundfläche.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl → Was bedeutet das?