Aufgaben zur Konstruierbarkeit von Dreiecken
Hier findest du Aufgaben zur Konstruierbarkeit von Dreiecken. Lerne, Konstruktionssätze anzuwenden und Sachprobleme zu lösen!
- 1
Entscheide, ob man aus folgenden Angaben eindeutig Dreiecke konstruieren kann.
Und wenn ja, konstruiere das Dreieck.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
Skizze anfertigen
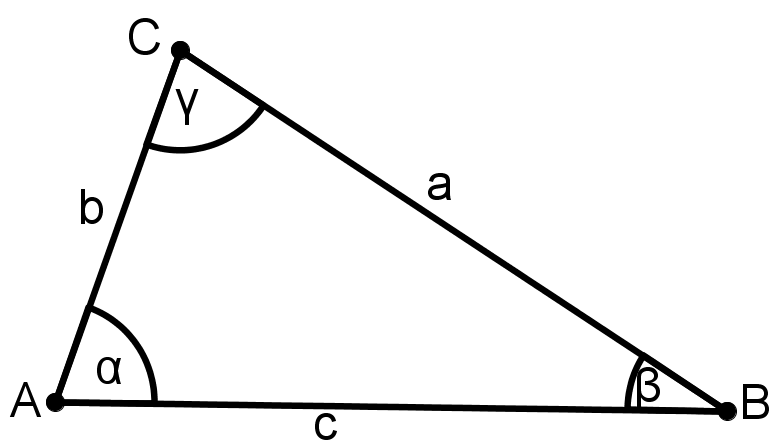
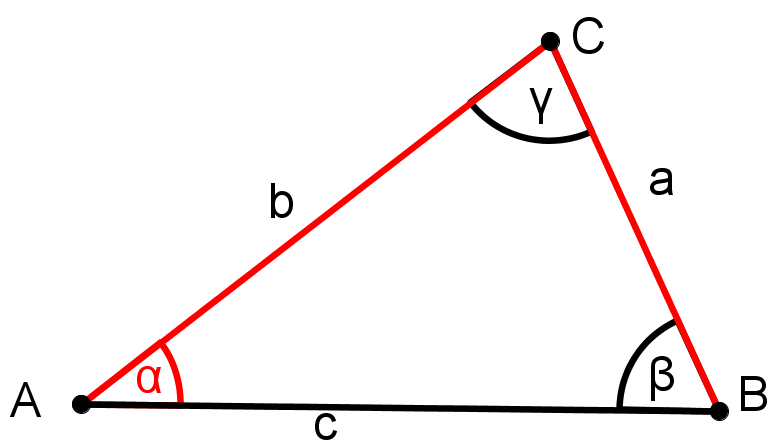
Benenne ein beliebiges Dreieck
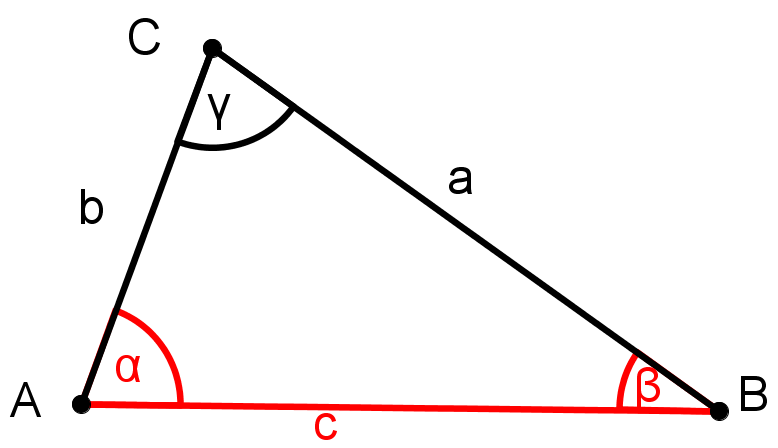
Markiere die bekannten Größen. Man sieht in der Skizze, dass das Dreieck die Voraussetzung des WSW-Satzes erfüllt. Deshalb ist es eindeutig konstruierbar.
Dreieck konstruieren
Hier findest du das Applet zur Konstruktion mithilfe des WSW-Satzes.

Zeichne eine Gerade und auf ihr irgendwo den Punkt A ein.

Zeichne einen Kreis um A, dessen Radius genauso groß ist wie die Länge der Seite c.
Der Schnittpunkt des Kreises mit der Geraden ist der Punkt B.
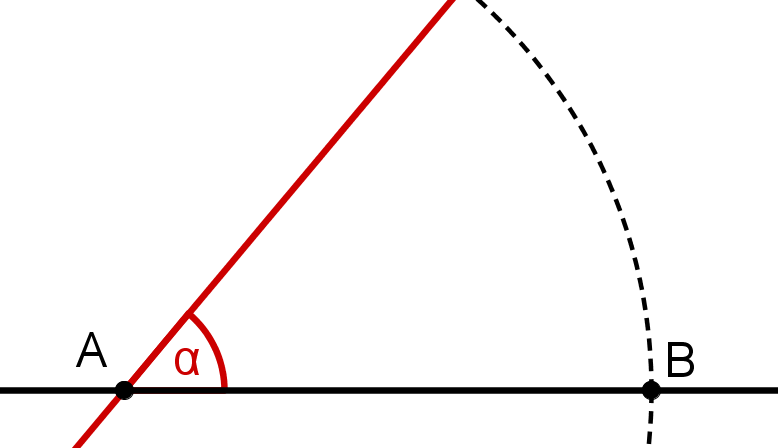
Zeichne an A einen 50° Winkel.
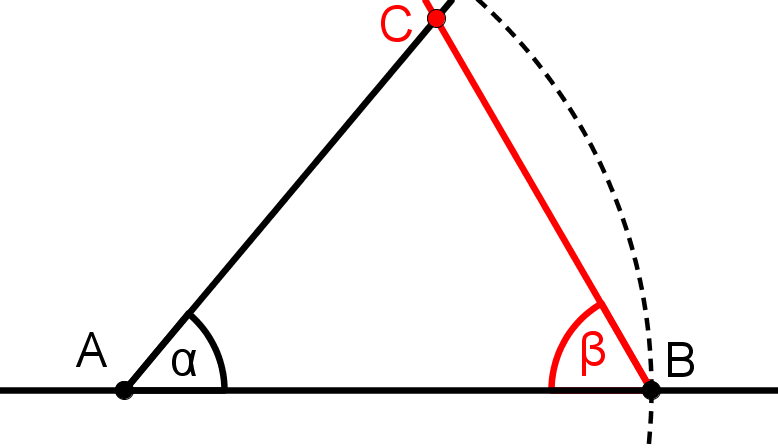
Zeichne an B einen 60° Winkel.
Der Schnittpunkt der beiden Schenkel ist der Punkt C des Dreiecks.
Somit hat man das Dreieck eindeutig konstruiert.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
Skizze anfertigen

Benenne ein beliebiges Dreieck
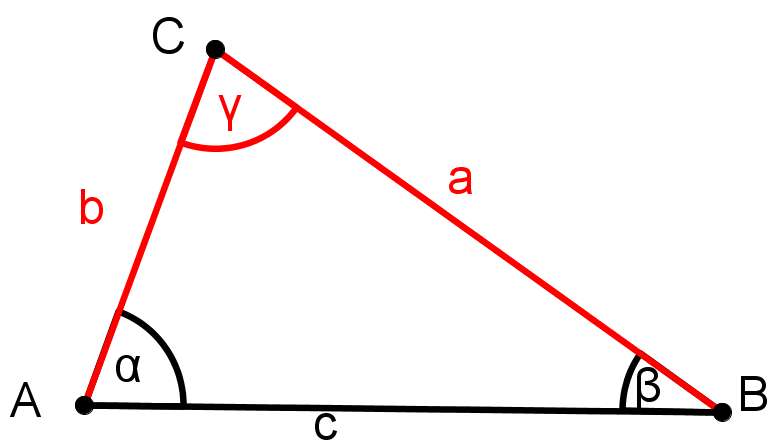
Markiere die bekannten Größen.
Man sieht in der Skizze, dass das Dreieck die Voraussetzung des SWS-Satzes erfüllt.
Deshalb ist es eindeutig konstruierbar.
Dreieck konstruieren
Hier findest du ein Applet zur Konstruktion mithilfe des SWS-Satzes.

Zeichne eine Gerade und auf ihr irgendwo den Punkt C ein.
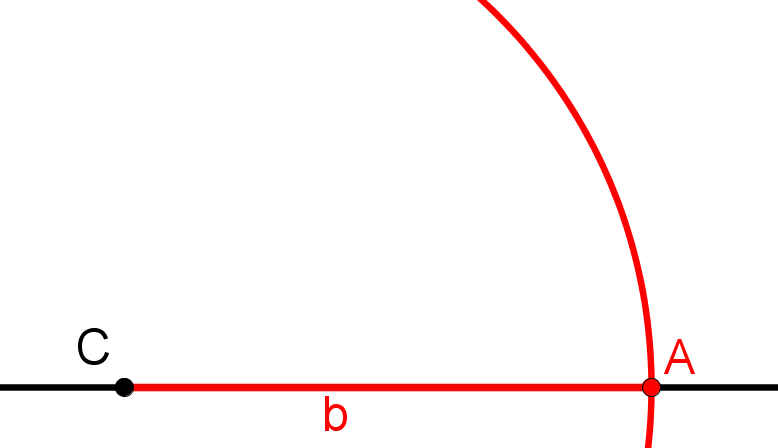
Zeichne einen Kreis um C, dessen Radius genauso groß ist wie die Länge der Seite b.
Der Schnittpunkt des Kreises mit der Geraden ist der Punkt A.
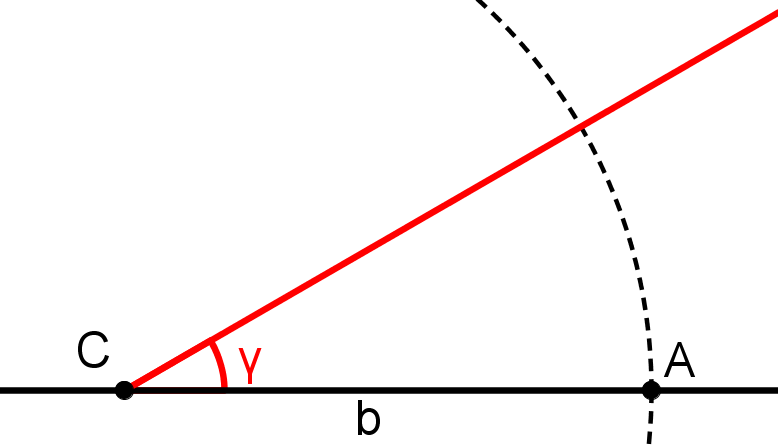
Konstruiere an C einen 30° Winkel .
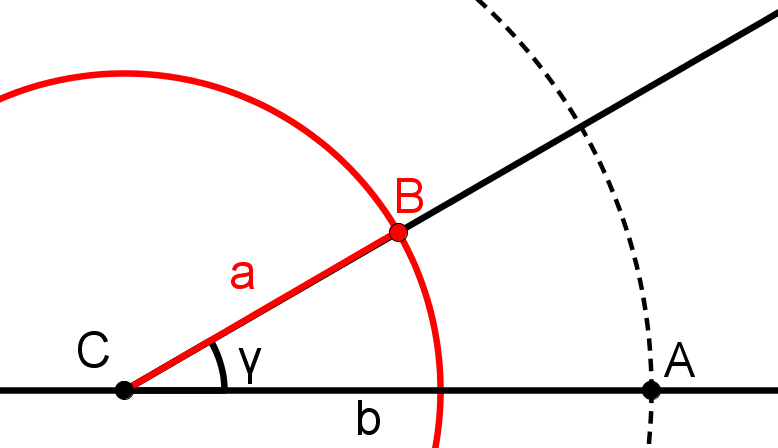
Zeichne um C einen Kreis, dessen Radius so groß ist wie die Seite a.
Der Schnittpunkt des Kreises mit dem eben konstruierten Schenkel ist der Punkt B.
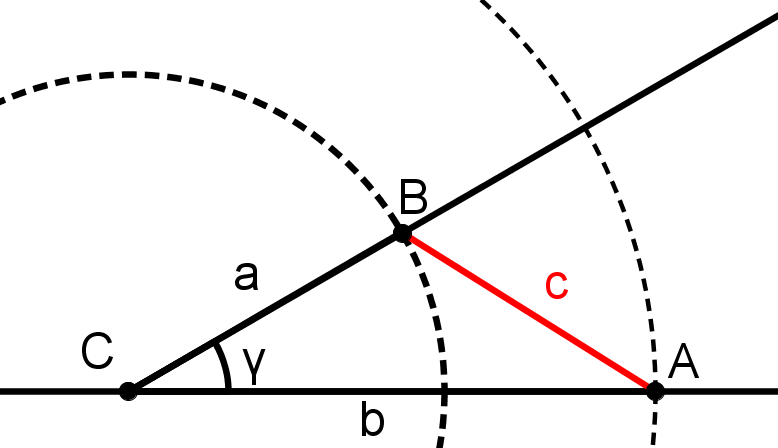
Verbinde die Punkte A und B. Diese Strecke ist die Seite c.
Das Dreieck ABC ist das gesuchte Dreieck.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
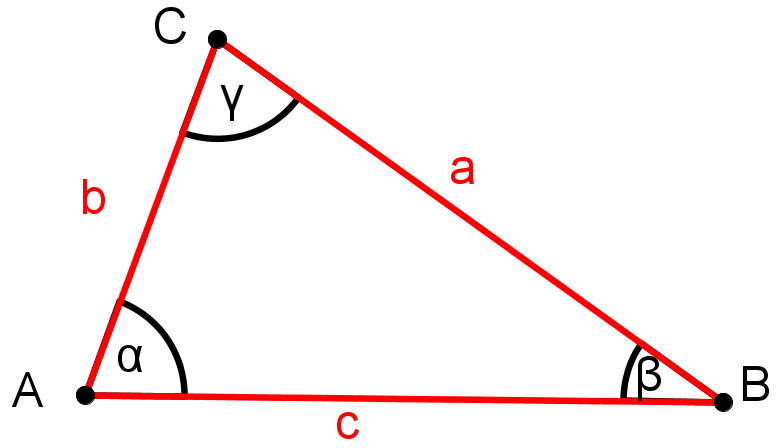
Skizze anfertigen

Benenne ein beliebiges Dreieck und markiere die bekannten Größen.
Laut Skizze kommt nur der SsW-Satz in Frage. Es muss also noch überprüft werden, ob die Seite, die dem gegebenen Winkel gegenüberliegt größer ist als die andere Seite.
Laut Angabe ist , weshalb die Voraussetzung des SsW-Satzes erfüllt ist.
Deshalb ist es eindeutig konstruierbar.
(VORSICHT: Würde man nur die Skizze betrachten, wäre )
Dreieck konstruieren
Hier findest du ein Applet zur Konstruktion mithilfe des SsW-Satzes.
Zeichne einen Strahl von einem Punkt aus und konstruiere einen Winkel von mit dem Scheitel bei .
Der Punkt liegt auf dem zweiten Schenkel des Winkels cm von entfernt.
Zeichne einen Kreis um mit dem Radius cm. Der Schnittpunkt dieses Kreises mit dem Strahl von aus ist der Punkt
Die Strecke AB ist die Seite c.
Verbinde den Punkt mit dem Punkt . Diese Strecke ist die Seite .
Das Dreieck ist das gesuchte Dreieck
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Konstruktion von Dreiecken
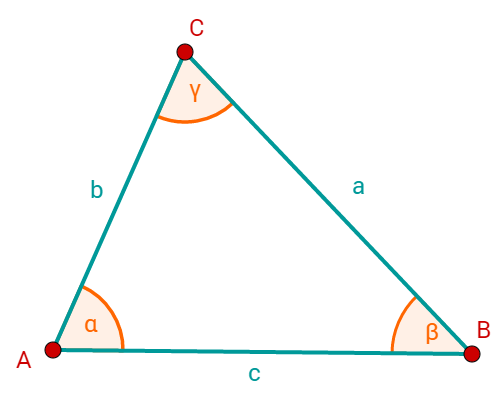
Skizze anfertigen

Benenne ein beliebiges Dreieck
Markiere die bekannten Größen.
Man sieht in der Skizze, dass das Dreieck die Voraussetzung des SSS-Satzes erfüllt.
Deshalb wäre es eindeutig konstruierbar.
ABER:
Dreiecksungleichung überprüfen
aber:
Da die Seite c größer als die Summe der anderen beiden Seiten ist, existiert dieses Dreieck nicht!

Versucht man das Dreieck dennoch zu konstruieren (ohne die Dreiecksungleichung beachtet zu haben), stellt man fest, dass sich die Kreise die den Seiten a und b entsprechen nicht schneiden, es also kein Punkt C gibt.
Hast du eine Frage oder Feedback?
- 2
Begründe, mit welchen der folgenden Angaben du ein Dreieck eindeutig konstruieren kannst! Zeichne dir dazu eine Skizze mit den gegebenen Werten auf!
, ,
Konstruierbarkeit des Dreiecks
Zeichne zuerst eine Skizze, von dem Dreieck (ähnlich, wie der in der Angabe).
Die türkisen Seiten sind gegeben. Überlege nun, welchem Kongruenzsatz das entspricht.
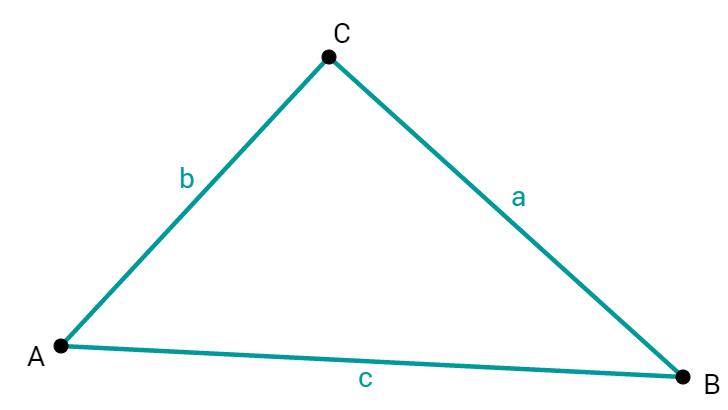
Das Dreieck entspricht dem SSS-Satz, ist also prinzipiell konstruierbar.
Überprüfe nun noch, ob die beiden kürzeren Seiten zusammen größer als die lange Seite ist. Nur dann existiert das Dreieck überhaupt!
Da ist, existiert das Dreieck und ist nach dem SSS-Satz auch konstruierbar!
Hast du eine Frage oder Feedback?
, ,
Konstruierbarkeit des Dreiecks
Zeichne zuerst eine Skizze, von dem Dreieck (ähnlich, wie der in der Angabe).
Die türkisen Seiten sind gegeben. Überlege nun, welchem Kongruenzsatz das entspricht.
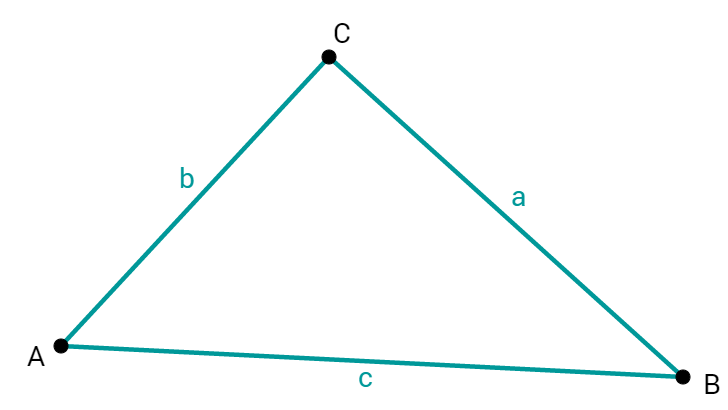
Das Dreieck entspricht dem SSS-Satz, ist also prinzipiell konstruierbar.
Überprüfe nun noch, ob die beiden kürzeren Seiten zusammen größer als die lange Seite ist. Nur dann existiert das Dreieck überhaupt!
Da sind, existiert das Dreieck nicht und du kannst es daher auch nicht konstruieren. Die beiden Seiten und haben keinen gemeinsamen Schnittpunkt.
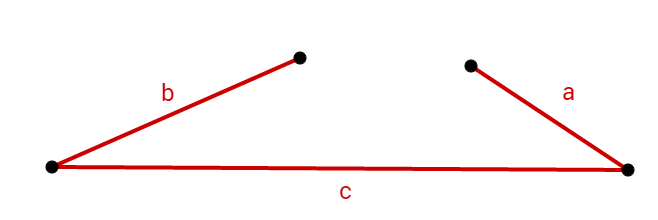
Hast du eine Frage oder Feedback?
Konstruierbarkeit des Dreiecks
Zeichne zuerst eine Skizze, von dem Dreieck (ähnlich, wie der in der Angabe) und markiere die gegebenen Größen.
Überlege, welchem Kongruenzsatz dieses Dreieck entspricht.
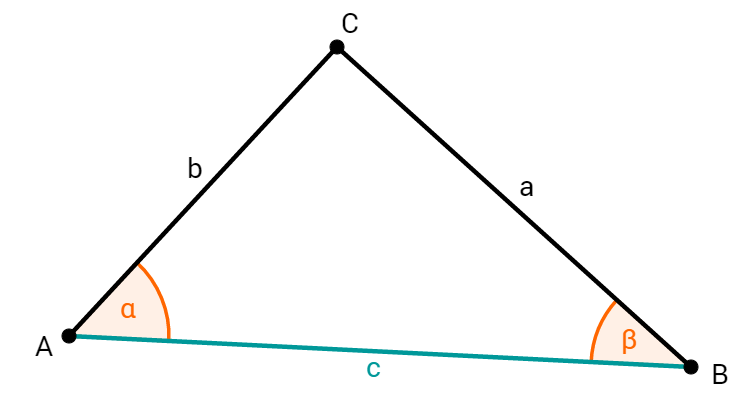
Da eine Seite und die zwei anliegenden Winkel gegeben sind, kannst du den WSW-Satz erkennen.
Dreiecke, die dem WSW-Satz entsprechen, sind eindeutig konstruierbar!
Hast du eine Frage oder Feedback?
Konstruierbarkeit des Dreiecks
Zeichne zuerst eine Skizze (ähnlich, der in der Angabe) und markiere alle gegebenen Größen.
Überlege nun, welchem Kongruenzsatz dieses Dreieck entspricht!
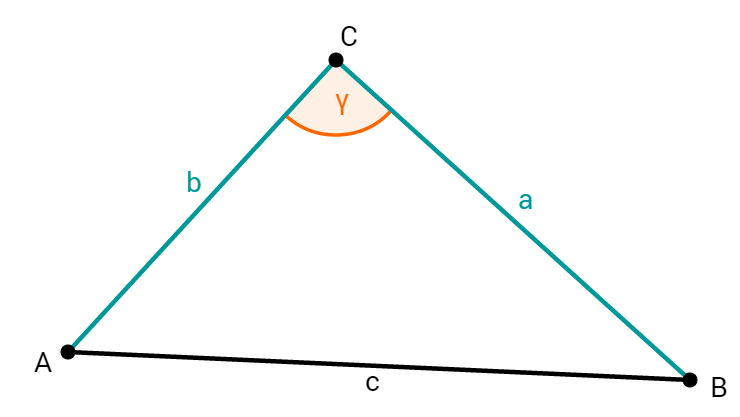
Du hast zwei Seiten und den Winkel dazwischen gegeben. Daher entspricht das Dreieck dem SWS-Satz!
Nach dem SWS-Satz ist das Dreieck eindeutig konstruierbar!
Hast du eine Frage oder Feedback?
Konstruierbarkeit des Dreiecks
Zeichne zuerst eine Skizze (ähnlich der in der Angabe) und markiere die gegebenen Größen.
Überlege nun, um welchen Kongruenzsatz es sich handeln könnte.
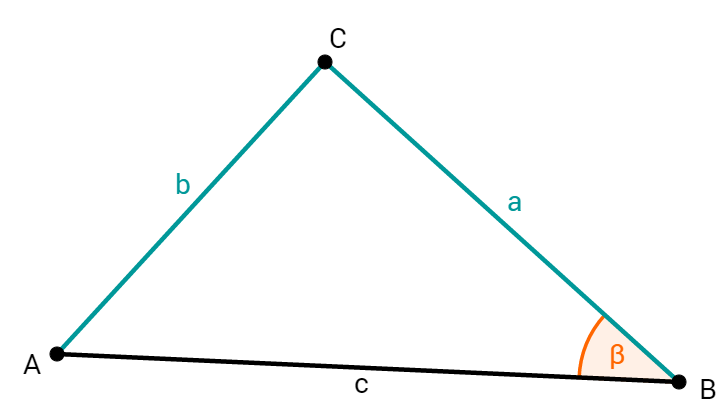
Du hast zwei Seiten und einen Winkel gegeben. Der Winkel liegt nicht zwischen den gegebenen Seiten. Es handelt sich also entweder um den SsW oder um den sSW Satz.
Überprüfe, ob der Winkel gegenüber der großen (SsW-Satz) oder gegenüber der kleinen (sSW-Satz) liegt.
Du kannst schnell sehen, dass die größere der beiden Seiten ist. Diese liegt gegenüber von .
Du weißt jetzt also, dass es sich um den SsW-Satz handelt.
Dreiecke, die dem SsW-Satz entsprechen, sind eindeutig konstruierbar. Deshalb weißt du, dass dieses Dreieck konstruierbar ist!
Hast du eine Frage oder Feedback?
Konstruierbarkeit des Dreiecks
Zeichne zuerst eine Skizze (ähnlich der in der Angabe) und markiere die gegebenen Größen.
Überlege nun, um welchen Kongruenzsatz es sich handeln könnte.

Du hast zwei Seiten und einen Winkel gegeben. Der Winkel liegt nicht zwischen den gegebenen Seiten. Es handelt sich also entweder um den SsW oder um den sSW Satz.
Überprüfe, ob der Winkel gegenüber der großen (SsW-Satz) oder gegenüber der kleinen (sSW-Satz) liegt.
Du kannst schnell sehen, dass die größere der beiden Seiten ist. Diese liegt neben .
Du weißt jetzt also, dass es sich um den sSW-Satz handelt.
Dreiecke, die dem sSW-Satz entsprechen, sind nicht eindeutig konstruierbar. Es gibt immer zwei Möglichkeiten, sie mit diesen Angaben zu zeichnen.
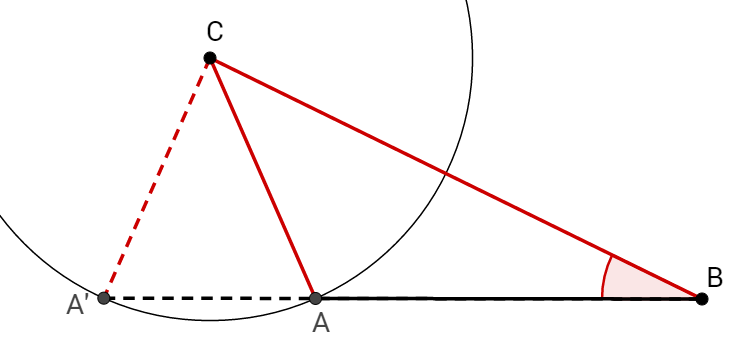
Hast du eine Frage oder Feedback?
Konstruierbarkeit des Dreiecks
Zeichne zuerst eine Skizze (ähnlich der in der Angabe) und markiere die gegebenen Größen.
Überlege nun, um welchen Kongruenzsatz es sich handelt.
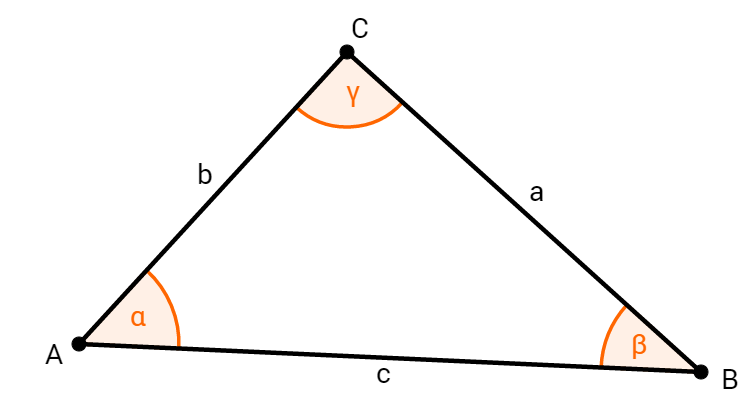
Alle drei Winkel sind angegeben, es handelt sich also um den WWW-Satz.
Dreiecke, sind nach dem WWW-Satz nicht eindeutig konstruierbar.
Es müsste noch eine Seite angegeben sein, um die Größe des Dreiecks zu bestimmen.
Hast du eine Frage oder Feedback?
- 3
Die zwei Freundinnen Julia und Lena fahren sehr gerne Skateboard. Julias Papa hat Julia eine Rampe gebaut und jetzt will Lena auch so eine!
Die beiden telefonieren miteinander und Julia erklärt Lena, wie die Rampe aussieht:
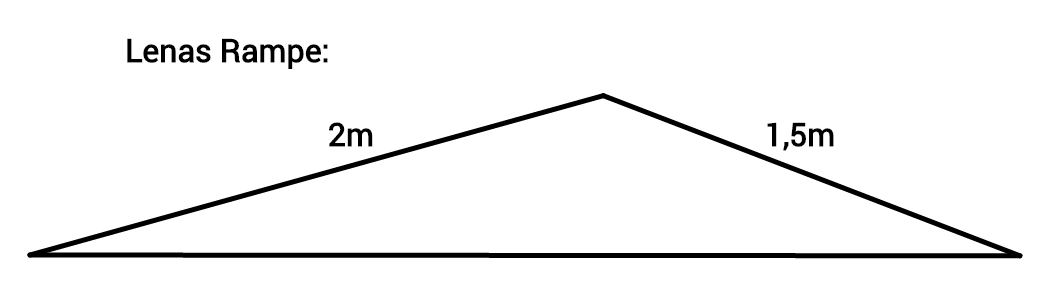
"Die Rampe besteht aus einem Brett, das lang ist und das andere ist lang. Das -Brett ist vorne, so dass du dann über das Brett runter fährst."
Lena zeichnet sich gleich eine Skizze und baut die Rampe:
Zwei Wochen später telefonieren die beiden nochmal:
Lena sagt: "Die Rampe ist langweilig! Sie ist überhaupt nicht steil genug!"
Julia: "Meine nicht, sie ist sogar so steil, dass man nur mit viel Anlauf drüber kommt!"
Sie mailen sich die Bilder der Rampen zu, um sie zu vergleichen:
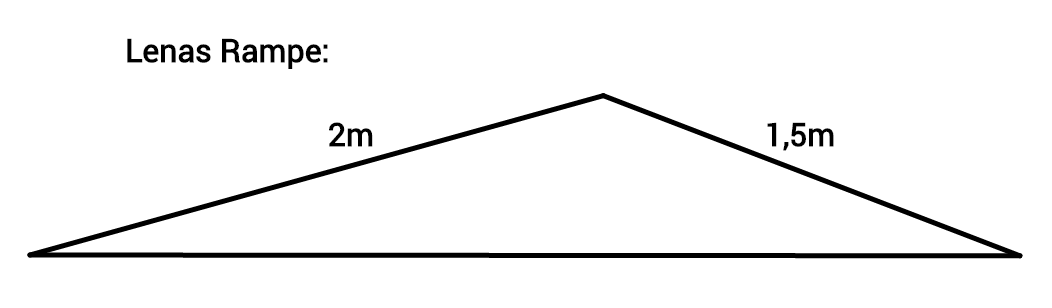
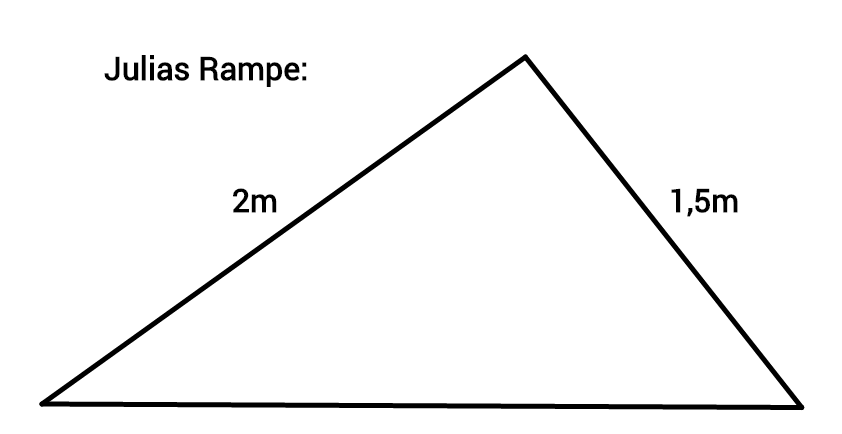
Warum sehen die beiden Rampen unterschiedlich aus?
Uneindeutigkeit der Angaben
Julia hat versucht, die Rampe nur mithilfe von zwei Angaben zu beschreiben. Die Rampe hat die Grundfläche eines Dreiecks, so dass man dieselben Kriterien für die Eindeutigkeit wie bei einem Dreieck annehmen kann.
Ein Dreieck ist durch zwei Angaben nicht eindeutig beschrieben und somit nicht konstruierbar. Lena hat diese zwei Strecken-Angaben in einem anderen Winkel zusammengebaut als Julia und somit eine andere Rampe erhalten.
Hast du eine Frage oder Feedback?
Welche weitere Angabe könnte Julia an Lena weitergeben, so dass sie die Rampe identisch nachbauen kann?
Eindeutigkeit der Rampe
Die Rampe hat die Grundfläche eines Dreiecks. Dieses muss eindeutig sein.
Dreiecke sind eindeutig, wenn ein Kongruenzsatz gegeben ist.
In diesem Fall hast du zwei Strecken bereits gegeben, du suchst also einen Kongruenzsatz mit zwei Strecken und kannst dann die dritte Angabe hinzufügen.
Mögliche Kongruenzsätze:
SWS
SsW
SSS
Überlege dir, welche Angabe Julia nun noch für die verschiedenen Kongruenzsätze ausmessen sollte.
Gehe davon aus, dass die Strecke mit die Strecke ist und die Strecke .
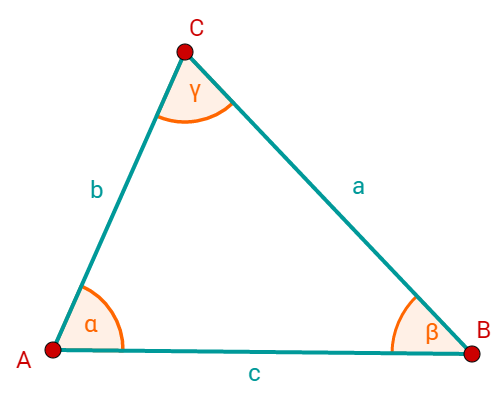
Für den SWS Satz wird der Winkel benötigt.
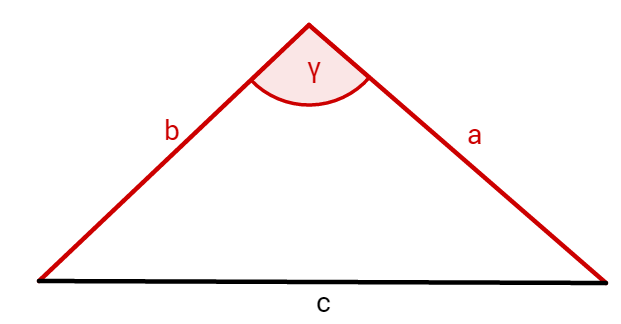
Für den SSS Satz wird die dritte Seite benötigt.
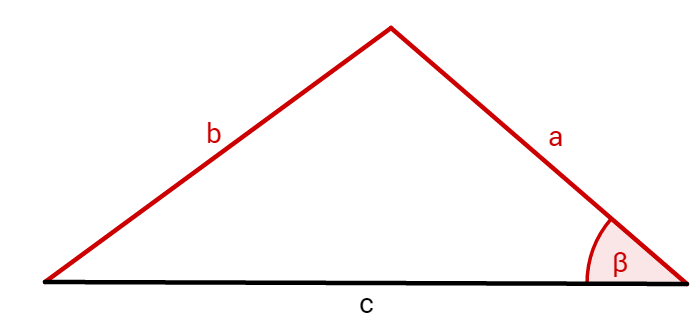
Für den SsW-Satz wird der Winkel benötigt.
Julia kann also eine der folgenden Angaben ausmessen:
den Winkel ,
die Strecke ,
den Winkel
Durch jede dieser drei Angaben wird das Dreieck eindeutig zu konstruieren und ist somit ausreichend beschrieben.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?


