Aufgrund der Kongruenzsätze reicht es für die eindeutige Konstruktion eines Dreiecks aus, wenn man nur Größen (Länge der Seiten und/oder Winkelgrößen) des Dreiecks kennt.
Ein Dreieck ist eindeutig konstruierbar, wenn man
die Längen aller Seiten (SSS-Satz) oder
die Länge zweier Seiten und die Größe des von ihnen eingeschlossenen Winkels (SWS-Satz) oder
die Länge einer Seite und die Größe der anliegenden Winkel (WSW-Satz) oder
die Längen zweier Seiten und die Größe des der längeren der beiden Seiten gegenüberliegenden Winkels (SsW-Satz)
kennt.
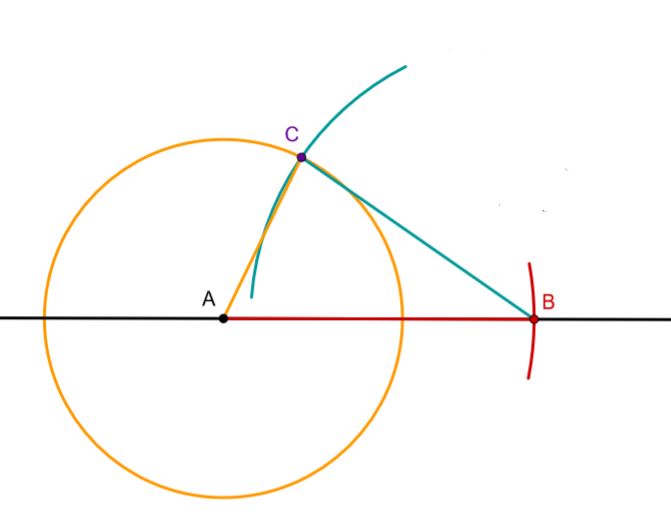
Wie du Dreiecke berechnen kannst, ist im Artikel Berechnung von Dreiecken mit Sinus- und Kosinussatz beschrieben.
Vorgehen bei der Konstruktion
Als konkretes Beispiel wird jetzt gewählt: Konstruktion eines Dreiecks mit den Seitenlängen:
Zuallererst fertigt man eine Skizze/Planfigur an.
Man zeichnet dazu ein beliebiges Dreieck, bei dem die Winkel und Längen nicht mit den Angaben übereinstimmen müssen, aber die Namen der Seiten und Winkel angegeben werden.
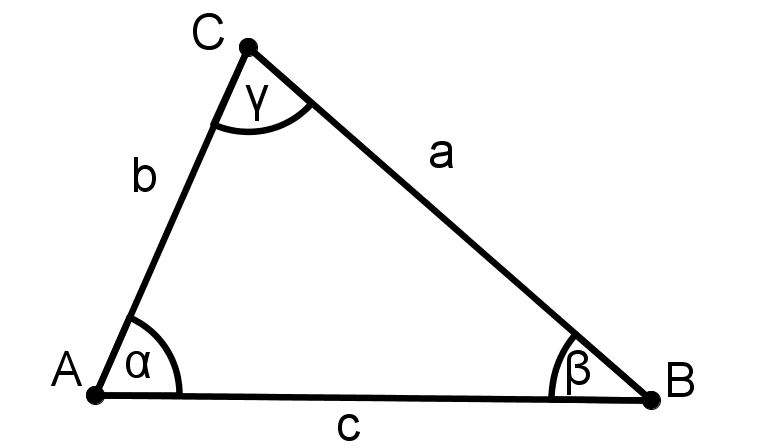
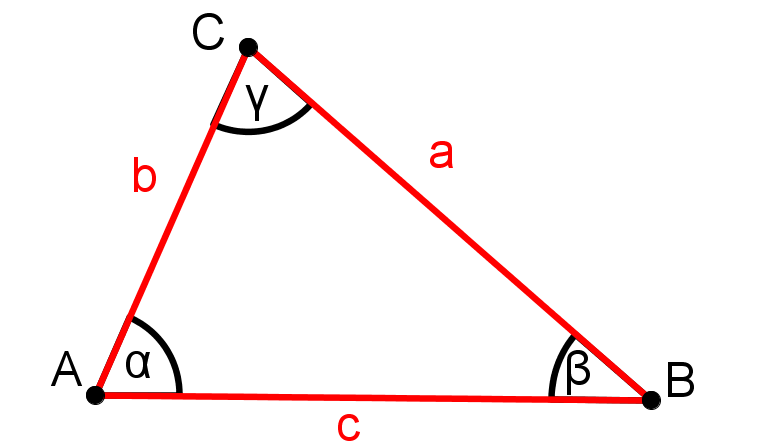
Man markiert nun die bekannten Größen und erkennt, ob die Angaben die Voraussetzungen eines Kongruenzsatzes erfüllen. Jetzt weiß man auch, ob man das Dreieck eindeutig konstruieren kann.
(in diesem Beispiel: SSS-Satz eindeutig konstruierbar)
Nun folgt die eigentliche Konstruktion. Es gibt immer unterschiedliche Herangehensweisen für die Konstruktion.
Beginne immer mit einer Seite und konstruiere dann die weiteren gegebenen Winkel oder Seiten.
Seitenlängen werden immer mit dem Zirkel eingetragen.
Winkel müssen je nach Angabe konstruiert werden oder dürfen mit dem Geodreieck gezeichnet werden.
Video zum Thema Dreieckskonstruktion mit dem SSS-Satz
Laden
Die Dreiecksungleichungen
Für jedes Dreieck gilt:
Die Länge einer Dreiecksseite muss immer kleiner sein als die Summe der Längen der anderen beiden Seiten. Formal aufgeschrieben:
Diese Ungleichungen sind besonders wichtig, wenn man drei Seitenlängen gegeben hat. Erfüllen die Angaben die Dreiecksungleichungen nicht, dann gibt es kein solches Dreieck. Es reicht aus, wenn man überprüft, ob die größte Seite kleiner als die Summe der anderen beiden Seiten ist. Damit sind die anderen beiden Ungleichungen automatisch auch erfüllt.
Konstruktionsbeispiele
Konstruiere ein Dreieck mit den Seitenlängen
Zeichne eine Gerade und wähle darauf den Punkt A des Dreiecks aus.
Zeichne einen Kreis um A, dessen Radius genauso groß ist wie die Seite c.
Der Schnittpunkt der Geraden und des Kreises ist der Eckpunkt B.
Zeichne einen Kreis um B, dessen Radius so groß ist wie die Seite a.
Zeichne einen Kreis um A, dessen Radius so groß ist wie die Seite b.
Der Schnittpunkt der beiden Kreise ist der Punkt C des Dreiecks.
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Konstruierbarkeit von Dreiecken
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
