1 Diagramme erfassen und auswerten
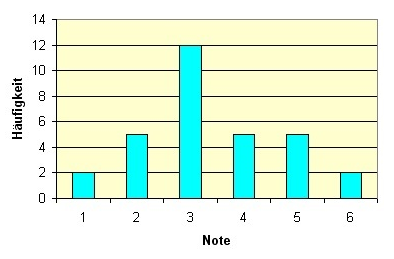
Unten stehendes Diagramm zeigt die Notenverteilungder letzten Mathematikschulaufgabe einer 5. Klasse:

Notenverteilung Matheschulaufgabe
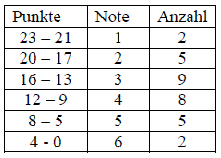
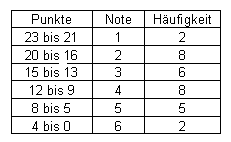
Die Informationen für dieses Diagramm wurden aus folgender Tabelle entnommen:
Um Informationen aus Listen und Tabellen übersichtlich darzustellen überträgt man diese in Diagramme. Dabei unterscheiden wir grundsätzlich drei Arten:
Säulendiagramm | Balkendiagramm | Liniendiagramm | |
|---|---|---|---|
Aussehen | 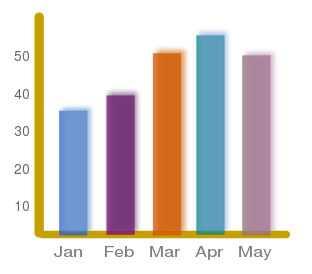 | 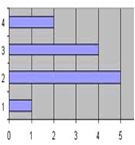 | 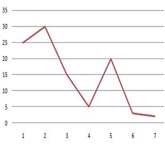 |
Wozu? | Darstellung eines Zustands | Darstellung eines Zustands | Darstellung eines Verlaufs |
Beispiel | Ausgaben eines Schülers | Notenverteilung in einer Klasse | Temperaturverlauf während eines Jahres |
Aufgabe 1:
Übertrage das Diagramm in dein Heft und beantworte die folgenden Fragen.
Fragen:
Wie viele Kinder haben die Note 3?
Wie viele Kinder haben die Note 1?
Wie viele Kinder haben eine schlechtere Note als 3?
Wie viele Schülerinnen und Schüler haben mitgeschrieben?
Aufgabe 2:
Übertrage die Tabelle in dein Heft und beantworte die folgenden Fragen.
Fragen:
Welche Art von Diagramm würdest du wählen?
Erstelle nun dein Diagramm. Achte dabei auf Achsenbeschriftung.
Aufgabe 3:
Nenne drei Beispiele aus deinem Alltag, bei denen du Informationen in einem Liniendiagramm darstellen würdest.
2 Kombinatorik
Bevor du mit diesem Baustein beginnst, musst du dir drei farbigen Kärtchen basteln!
Lege deine farbigen Kärtchen nun in unterschiedlichen Reihenfolgen auf deinen Tisch.

Übertrage nun alle gefunden Kombinationen in dein Heft. Dazu kannst du entweder mit Farben arbeiten, oder einfach für Rot = R, Blau = B und Grün = G schreiben.
Aufgabe:
Wie viele Kombinationsmöglichkeiten hast du gefunden?
Die verschiedenen Möglichkeiten, wie man die Kärtchen legen kann, können auch wie in folgendem Beispiel dargestellt werden:
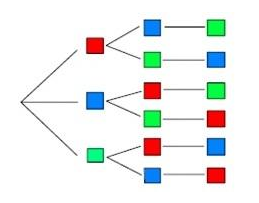
Dieses Beispiel zeigt dir, dass man beim ersten Legen Karten zur Auswahl hat, dann noch Karten und am Ende natürlich nur noch eine Karte.
Berechnen kann man also alle Kombinationsmöglichkeiten nach dem Schema:
Es gibt also 6 Kombinationsmöglichkeiten.
Aufgabe:
Wie viele Kombinationsmöglichkeiten hast du, wenn du zu Beginn 4 Farbkarten hättest?
Übungsaufgaben:
Aufgabe 1:
Bärbel möchte bei ihrer nächsten Geburtsparty kleine Spießchen aus Cracker, Käse und Tomate herstellen.
Wie viele Freunde hat Bärbel eingeladen, wenn jeder von ihnen ein Spießchen mit unterschiedlicher Steckreihenfolge der Zutaten bekommt? Bärbel isst natürlich auch einen Spieß.

Aufgabe 2:
Klaus kommt nach Hause und erzählt seiner Mutter, dass er in Deutsch (D), Englisch (E), Mathematik (M) und Geschichte (G) Hausaufgaben hat.

a) Er überlegt, welche Kombinationsmöglichkeiten es für seine Hausaufgabenreihenfolge es gibt. Schreibe alle auf!
b) Zeige durch Rechnung, dass er Kombinationsmöglichkeiten hat.
c) Wie viele Kombinationsmöglichkeiten gäbe es, wenn Klaus auch noch Biologiehausaufgaben zu erledigen hätte?
3 Übungen zum Thema Daten und Zufall
Bei einer Umfrage in einer 5. Klasse zum Thema "Lieblingsessen" ergibt sich folgende Tabelle:
Lieblingsessen | Anzahl |
|---|---|
Pizza | 9 |
Nudelgerichte | 4 |
Döner | 4 |
Süßspeisen | 2 |
Sonstiges | 5 |
Aufgaben:
Welche Art Diagramm würdest du wählen? Begründe kurz!
Erstelle nun dein Diagramm. Achte dabei auf die Achsenbeschriftung
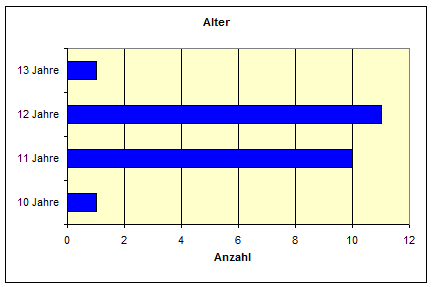
In der 5. Klasse ergibt sich folgende Altersverteilung:
Aufgaben:
Wie viele Kinder in der Klasse sind 11 Jahre alt?
Wie viele Kinder in der Klasse sind 12 Jahre alt?
Wie viele Kinder in der Klasse sind älter als 11 Jahre?
Wie viele Kinder sind insgesamt in der Klasse?
Aus drei verschiedenen Bausteinen soll ein Turm gebaut werden.
Aufgaben:
Berechne die Anzahl der verschiedenen Kombinationsmöglichkeiten, um den Turm zu bauen.
Zeichne alle möglichen Kombinationen. Dazu kannst du entweder mit Farben arbeiten, oder einfach für rot=R, blau=B und gelb=G schreiben