Wie erkennst du, ob ein bestimmtes Wort von einem bestimmten regulären Ausdruck erzeugt wird? Dies ist im Allgemeinen gar nicht so einfach. Das Konzept des endlichen Automaten hilft dabei.
Der reguläre Ausdruck a(a|b)a erzeugt alle Wörter, die mit a anfangen, dann mit beliebig vielen a's oder b's weitergehen und zum Schluss mit a enden.
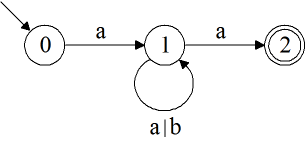
Du kannst diesen regulären Ausdruck grafisch mit einem Diagramm darstellen. Die Kreise in dem Diagramm heißen Zustände. In folgendem Diagramm gibt es die Zustände 0, 1 und 2. Die Pfeile heißen Zustandsübergänge.
Wörter erzeugen
Wenn du das Diagramm von links nach rechts durchläufst, erzeugst du entsprechende Wörter, indem du die Zeichen aneinanderreihst, an denen du vorbeikommst.
Du startest im Zustand 0 und gehst den Pfeil entlang zum Zustand 1. Dabei erzeugst du ein a. Dann kreist du beliebig oft im Zustand 1 und reihst dabei a's und b's an. Und zum Schluss gehst du zum Zustand 2 und reihst noch ein a an.
So kannst du beispielsweise Wörter wie abba oder aaaaa erzeugen.
Wörter erkennen
Mit demselben Diagramm kannst du diese Wörter auch erkennen. Stell dir vor, dass du ein solches Wort zeichenweise einliest.
Du startest im Zustand 0. Wenn du als erstes Zeichen ein a liest, gehst du den Pfeil entlang zum Zustand 1. Solange du weitere a's oder b's liest, kreist du im Zustand 1. Mit dem letzten gelesenen a gehst du zum Zustand 2.
Der Zustand 2 ist durch den doppelten Kreis als Endzustand gekennzeichnet. Du erkennst ein Wort, wenn du
es vollständig eingelesen hast und
einen Endzustand erreicht hast.
Das ist schon alles. Damit hast du das Prinzip des nichtdeterministischen endlichen Automaten verstanden.
Du liest ein Eingabewort zeichenweise ein und vollführst dabei entsprechende Zustandsübergänge. Achte darauf, dass du dabei nur Pfeile entlang gehst, die mit dem jeweils gelesenen Zeichen markiert sind.
Nichtdeterminismus
Was ist aber, wenn es keinen solchen Pfeil gibt? Zum Beispiel, wenn du im Zustand 0 bist und ein b liest? Dann brichst du ab. Dann weißt du, dass du es mit einem Wort zu tun hast, das nicht zu der Sprache gehört, in diesem Fall ein Wort, das mit b anfängt.
Und was ist, wenn es mehrere Pfeile gibt, die du entlang gehen kannst? Du bist im Zustand 1 und liest ein a. Was machst du? Kreist du im Zustand 1 oder gehst du zum Zustand 2?
Hier kommt der Nichtdeterminismus ins Spiel. Du entscheidest dich nichtdeterministisch. Dies bedeutet:
du gehst mit schlafwandlerischer Sicherheit den richtigen Pfeil entlang oder
du gehst beide Pfeile gleichzeitig entlang
Dies sind die beiden Möglichkeiten, mit Nichtdeterminismus umzugehen.
Die erste Möglichkeit bedeutet Folgendes: Du kennst oder errätst eine Lösung (hier: den richtigen Weg durch das Diagramm), und du überprüfst sie noch einmal, d. h. du weist nach, dass sie tatsächlich eine Lösung ist.
Die zweite Möglichkeit bedeutet Folgendes: Sobald du mehrere nichtdeterministische Wahlmöglichkeiten hast, klonst du die aktuelle Situation entsprechend oft und rechnest entweder parallel oder nacheinander mit diesen Situationen weiter.
Nichtdeterminismus ist eigentlich nichts Besonderes. Schau dir einen Stadtplan an. Er zeigt dir nicht, welchen Weg du von zu Hause zum Bahnhof einschlagen musst – er zeigt dir nur, wie du gehen kannst. Du kannst den kürzesten Weg nehmen, du kannst einen Schlenker durch den Park machen, du kannst unterwegs mehrmals einen Häuserblock umrunden…
Deterministisch und nichtdeterministisch verhalten sich zueinander wie müssen und können.
Es gibt auch deterministische endliche Automaten. Bei einem deterministischen endlichen Automaten gibt es für jeden Zustand und jedes Eingabezeichen genau einen Folgezustand. Du kannst aus einem nichtdeterministischen endlichen Automaten einen deterministischen endlichen Automaten konstruieren, der dieselbe Sprache erkennt, mithilfe der sogenannten Teilmengenkonstruktion.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
