Nichtdeterministische endliche Automaten haben im Allgemeinen weniger Zustände als entsprechende deterministische Automaten. Und sie sind paradoxerweise oft intuitiver anzugeben – sie haben also ihre Berechtigung, auch wenn Nichtdeterminismus schwerer zu verstehen ist.
Aber es stellt sich heraus, dass die nichtdeterministischen endlichen Automaten, obwohl sie allgemeiner definiert sind, nicht "mehr können" als die deterministischen endlichen Automaten:
Zu jedem nichtdeterministischen endlichen Automaten gibt es einen deterministischen endlichen Automaten, der dieselbe Sprache erkennt.
Diese Tatsache lässt sich anschaulich sehr gut darstellen.
Arbeitsweise eines nichtdeterministischen endlichen Automaten
Am besten vergegenwärtigst du dir zunächst noch einmal das Verhalten eines nichtdeterministischen endlichen Automaten mit folgendem Zustandsdiagramm:
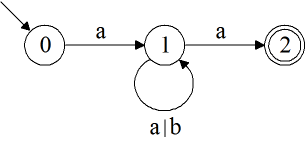
Dieser Automat ist kein deterministischer, endlicher Automat – denn dazu müsste zu jedem Zustand und jedem Eingabezeichen genau ein eindeutiger Folgezustand definiert sein. Dies ist nicht der Fall, denn
zum Zustand 0 und Eingabezeichen b ist kein Folgezustand definiert,
zum Zustand 1 und Eingabezeichen a sind zwei Folgezustände definiert,
zum Zustand 2 ist mit keinem Eingabezeichen ein Folgezustand definiert.
Der Automat erkennt die reguläre Sprache a(a|b)*a, bestehend aus allen Wörtern, die mit a anfangen, dann mit beliebig vielen a's oder b's weitergehen und mit a enden.
Ein solches Wort ist beispielsweise abba. Du durchläufst das Zustandsdiagramm beginnend beim Startzustand 0 entlang von Pfeilen, die mit a-b-b-a bezeichnet sind, und endest im Endzustand 2.
Wichtig dabei ist, dass du mit dem letzten a nicht weiter im Zustand 1 kreist, sondern nach rechts zum Zustand 2 abbiegst. Diese Entscheidung triffst du nichtdeterministisch, also sozusagen "mit schlafwandlerischer Sicherheit", denn wissen kannst du nicht, ob das gerade gelesene a das letzte Zeichen des Wortes ist oder ob noch weitere Zeichen folgen.
Möglicherweise ist dir diese schlafwandlerische Sicherheit nicht gegeben ;-). Daher gibt es noch die Möglichkeit der Simulation.
Einen nichtdeterministischen endlichen Automaten simulieren
Stell dir das Zustandsdiagramm als Mensch-ärgere-dich-nicht-Spielbrett vor. Du willst das Wort abba erkennen. Als Erstes markierst du das Startfeld 0 mit einer Spielfigur:
Wenn du jetzt das erste Zeichen a einliest, rückst du die Spielfigur entlang des mit a bezeichneten Pfeils auf das Feld 1 vor:

Mit dem nächsten Zeichen b kreist du mit der Spielfigur im Feld 1 und mit dem darauffolgenden b noch einmal. Was aber nun, wenn du das Zeichen a liest? Kreist du im Feld 1 oder rückst du die Spielfigur auf Feld 2 vor?
Eine Strategie, um mit Nichtdeterminismus umzugehen, besteht darin, dass du alle Wahlmöglichkeiten parallel durchspielst. Du machst also beides. Du klonst die Spielfigur und lässt die eine Kopie im Feld 1 kreisen und rückst die andere auf Feld 2 vor:

Nun sind zwei Felder des Spielbretts mit einer Spielfigur markiert. Eines dieser Felder ist der Endzustand 2, du hast damit das Wort abba erkannt.
Angenommen, es folgt noch ein weiteres Zeichen, zum Beispiel noch ein a. Dann machst du mit beiden Spielfiguren wieder dasselbe: Du klonst die Spielfigur, die auf Feld 1 steht, und lässt die eine Kopie im Feld 1 kreisen und rückst die andere auf Feld 2 vor. Die Spielfigur, die auf Feld 2 steht, kann nicht weiterrücken, du entfernst sie. Es entsteht also dieselbe Situation wie vorher.
Das jeweils eingelesene Wort wird genau dann erkannt, wenn der Endzustand 2 mit einer Spielfigur markiert ist.
Formales Vorgehen
Technisch gesehen machst du bei der Simulation für jedes mit einer Spielfigur markierte Feld das Folgende:
du entfernst die Markierung von dem Feld und
markierst stattdessen alle Folgefelder, zu denen ein Pfeil hinführt, der mit dem gelesenen Zeichen bezeichnet ist.
Dies führt zu den drei unterschiedlichen "Spielzügen", die du bereits gesehen hast:
du rückst die Spielfigur vor oder
du klonst die Spielfigur mehrfach und rückst die neu geschaffenen Spielfiguren vor oder
du entfernst die Spielfigur.
Einen deterministischen endlichen Automaten konstruieren
Diese Simulation eines nichtdeterministischen endlichen Automaten ist ein deterministischer Vorgang – du weißt in jeder Situation, was du zu tun hast, du brauchst nicht zu raten oder schlafzuwandeln.
Das, was bei der Simulation geschieht, ist im Grunde genommen das Verhalten eines deterministischen endlichen Automaten. Die Zustandsmenge dieses deterministischen Automaten besteht dabei aus den "Momentaufnahmen", die bei der Simulation des nichtdeterministischen Automaten entstehen (die obigen Bilder, zusätzlich das folgende Bild); hieraus ergibt sich auch die Übergangsrelation (die nun eine Übergangsfunktion ist). Die Momentaufnahme des folgenden Bilds entsteht, wenn du im Zustand 0 das Zeichen b liest. Dann entfernst du die Spielfigur von Feld 0. Jede Momentaufnahme, in der ein Endzustand markiert ist, ist ein Endzustand des deterministischen Automaten.
Hier siehst du das Zustandsdiagramm des deterministischen endlichen Automaten, der auf diese Weise aus dem nichtdeterministischen endlichen Automaten konstruiert ist. Du siehst, dass bei diesem Automaten für jeden Zustand und jedes Eingabezeichen genau ein Zustandsübergang definiert ist. Der Automat ist daher deterministisch. Aufgrund seiner Konstruktion erkennt er dieselbe Sprache.
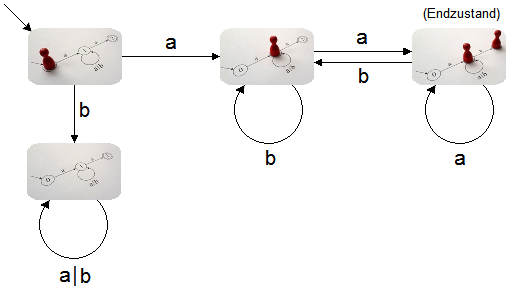
Die Momentaufnahmen entsprechen Teilmengen von markierten Zuständen des nichtdeterministischen Automaten, daher wird dieses Verfahren als Teilmengenkonstruktion bezeichnet.
Etwas formaler mit diesen Teilmengen sieht der Automat folgendermaßen aus:
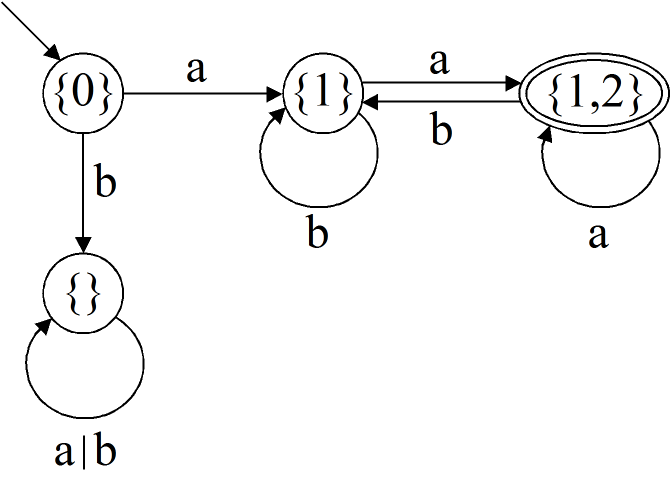
Und da es am Ende nicht mehr darauf ankommt, aus welchen Teilmengen die Zustände hervorgegangen sind, nummerierst du die Zustände einfach. Dann sieht der deterministische Automat so aus:
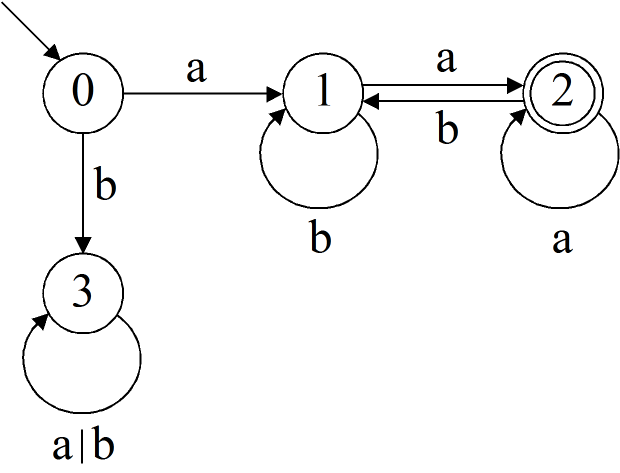
Mit der Teilmengenkonstruktion konstruierst du also aus einem beliebigen nichtdeterministischen endlichen Automaten einen deterministischen endlichen Automaten, der dieselbe Sprache erkennt.
